ANEJO 7: Cálculo simplificado de secciones en Estado Límite de Agotamiento frente a solicitaciones normales

1. Alcance

Las expresiones de este anejo son válidas únicamente para secciones con hormigón de resistencia fck≤ 50 N/mm2.

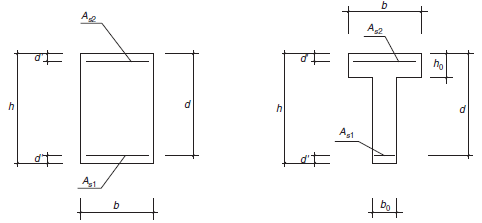
Figura A.7.1.

2. Hipótesis básicas y limitaciones

Las fórmulas que se presentan en los apartados siguientes se han deducido a partir de las hipótesis básicas expuestas en 42.1.2 adoptando un diagrama bilineal para el acero de la armadura pasiva y un diagrama parabólico- rectangular para el hormigón comprimido (aproximado para el cálculo de resultantes de tensiones y momentos por un diagrama rectangular, tal como se expone en 39.5).

Asimismo se han tenido en cuenta los dominios de deformación de agotamiento, que identifican el Estado Límite Último de Agotamiento frente a solicitaciones normales, de acuerdo con los criterios expuestos en 42.1.3.

Las fórmulas expuestas son válidas para los distintos tipos de acero para armadura pasiva, permitidos en esta Instrucción, siempre que se cumpla:

d' / d ≤ 0.20
d / h ≥ 0.80

A continuación, se define el significado de algunas variables utilizadas en las fórmulas de los siguientes apartados.

• Us1 = As1 · fyd
• Us2 = As2 · fyd
• fcd = αcc · fck / γc (art. 39.4, αcc = 1)
• Uo = fcd · b · d
• Uv = 2· Uo · d' / d
• Ua = fcd · b · h
  

Las fórmulas de este Anejo han sido obtenidas considerando que:

• La deformación del límite elástico del acero es εy = 0,002
• La deformación máxima del hormigón comprimido es 0,0033 en lugar de 0,0035.

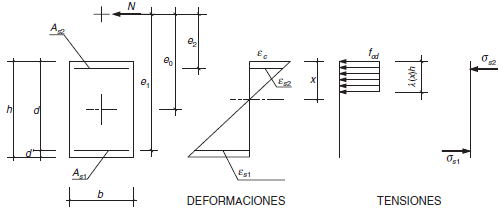
Figura A.7.3.

3. Flexión simple en sección rectangular
3.2. Comprobación

1.- Us1 - Us2 < Uv

2.- Uv ≤ Us1 - Us2 ≤ 0.5Uo

3.- 0.5Uo < Us1 - Us2

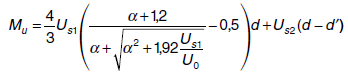
donde:

En el caso 1º, la situación de la fibra neutra está comprendida entre 0 < x < 2.5 d'. En el caso 2º, la situación de la fibra neutra está comprendida entre 2.5d' ≤ x ≤ 0.625 d. En el caso 3º, la situación de la fibra neutra está comprendida entre 0,625 d < x < d.

---

NOTAS

Flexión compuesta

Se aplica el método de Ehlers:

Todo problema de flexión compuesta, puede reducirse a uno de flexión simple, sin más que tomar como momento el que produce el esfuerzo normal con respecto a la armadura de tracción Md=Nd · e.

---

5. Dimensionamiento y comprobación de secciones rectangulares sometidas a flexión compuesta recta. Armadura simétrica dispuesta en dos capas con recubrimientos iguales.
5.2. Comprobación

1.- e_o < 0

,   Mu = Nu · e_o

2.- Us1(d-d') + 0.125Uo(d + 2d' - 4e_o) ≤ 0

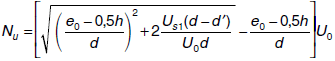,   Mu = Nu · e_o

3.- Us1(d-d') + 0.125Uo(d + 2d' - 4e_o) > 0

,   Mu = Nu · e_o

con:

donde:

6. Flexión esviada simple o compuesta en sección rectangular

El método que se propone permite el cálculo de secciones rectangulares, con armadura en sus cuatro esquinas y armaduras iguales en las cuatro caras, mediante la reducción del problema a uno de flexión compuesta recta con una excentricidad ficticia, tal como se define seguidamente (figura A.7.4).

donde: ey / ex ≥ h / b,

y β se define en la tabla siguiente:

Tabla A.7.6

v = Nd / (b·h·fcd)	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	≥0,8
β	0,5	0,6	0,7	0,8	0,9	0,8	0,7	0,6	0,5

Para cuantías grandes (w >0,6) los valores indicados para β se aumentarán 0,1 y para valores pequeños de cuantía w < 0,2 los valores de β se disminuirán en 0,1.

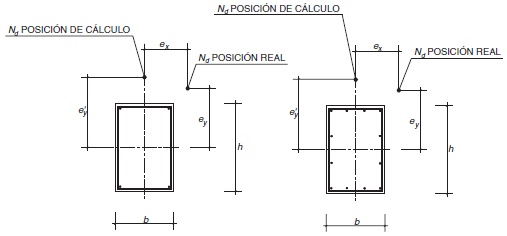
Figura A.7.4.