CTE SE-F: Muro fábrica con carga vertical
5.2 Muros sometidos predominantemente a carga vertical
Todo muro de carga tendrá un espesor de al menos 115 mm.
5.2.2 Capacidad portante
- En todo paño de un muro de fábrica, la compresión vertical de cálculo, Nsd, será menor o igual que su resistencia vertical de cálculo, NRd, es decir:
NSd ≤ NRd(5.5) - En muros de una hoja (o de dos hojas unidas rígidamente), la capacidad resistente vertical de cálculo a compresión vertical, NRd, por unidad de longitud, vale:
NRd= Φ·t·fd(5.6) - Φ es el factor de reducción del grueso del muro por efecto de la esbeltez y/o de la excentricidad de la carga que se calcula según el apartado 5.2.3.
- t es el espesor del muro
- fd es la resistencia de cálculo a compresión de la fábrica. Cuando el área A, en m2, de la sección horizontal de un muro sea menor que 0,1m2, se reducirá por el factor 0,7+3·A
- En muros capuchinos se comprobará cada hoja por separado.
donde:
5.2.3 Factor de reducción Φ
- En cabeza y base de muro, el factor de reducción, Φ, vale:
en cabeza Φ = 1 − 2·e/t(5.7) - a: la profundidad con que se remete la tabica del forjado respecto a la cara exterior del muro (figuras
5.2 y 5.3)
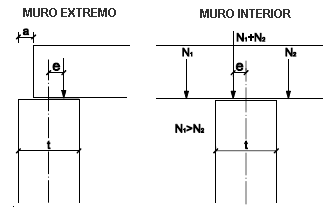
Figura 5.3 Excentricidad de apoyo en cabeza de muro superior - e: la excentricidad total de la sección que se comprueba. Salvo que se haya obtenido por capacidad, se considerará:
e = MSd/NSd+ ea > 0,05·t(5.9)donde:
- MSd: es el momento flector de cálculo de la sección que se comprueba, deducido del modelo estructural adoptado, debido a carga vertical, más, en su caso, el debido a las acciones laterales locales, según 5.5
- NSd: es el esfuerzo normal de cálculo en la sección que se comprueba, deducido del modelo estructural, en general considerando las plantas superiores sin sobrecarga.
- ea: es un incremento de excentricidad por ejecución. Si la categoría de ejecución es la B, ea = hd /450. Si la categoría de ejecución es la A, ea = hd /500. Si la categoría es la C, se adoptará el valor ea = 20 mm, si se trata de un tramo entre forjados y ea = 50 mm, si corresponde a un tramo libre en su extremo superior o su altura es la total del edificio. En las expresiones anteriores, hd es la altura de cálculo del muro, según el apartado 5.2.4. - La formulación completa para la determinación de Φ a media altura del muro se encuentra en el Anejo D.
- e: es la excentricidad debida a las solicitaciones en ese punto, según (5.9),
- ep la excentricidad debida a pandeo, de valor
ep = 0,00035 · t · (hd / td)2(5.12) - La excentricidad por fluencia puede considerarse nula para muros ejecutados con piezas cerámicas o de piedra natural, y en muros ejecutados con otro tipo de piezas con esbeltez menor o igual a 15. Para tener en cuenta la fluencia, el valor ep se incrementará en:
Δep = 0.002·φ∞·hd/td·√(t·em)(5.13)donde:
- hd es la altura de cálculo, según el apartado 5.2.4
- td es el espesor de cálculo del muro, según 5.2.5
Tabla 4.7 Deformabilidad de las fábricas
Tipo de pieza Coeficiente final de fluencia, φ∞ Cerámica 1,0 Silico-calcáreos 1,5 Hormigón ordinario y piedra artificial 1,5 Hormigón de árido ligero 2,0 Hormigón celular de autoclave 1,5 Piedra natural 1,0
Anejo D. Determinación del factor Φ a media altura de un muro
El valor del coeficiente Φ, a media altura de un muro se obtiene a partir de la expresión:
donde:
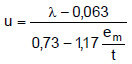
donde:
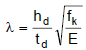
siendo:
exp: base de los logaritmos neperianos
em excentricidad por pandeo/fluencia,
donde:
hd: altura eficaz del muro, según 5.2.4,
td: espesor eficaz del muro, según 5.2.5,
fk: resistencia característica de la fábrica,
E: módulo de elasticidad de la fábrica. (Art. 4.6.5-2: Como módulo de elasticidad secante instantáneo, E, de una fábrica puede tomarse igual a 1000 fk.
5.2.4 Altura de cálculo de un muro
La altura de cálculo, hd, de un paño de muro de altura h, longitud L, y grueso t, puede determinarse según lo establecido en el Anejo E
Anejo E. Determinación de la altura de cálculo de un muro
La altura de cálculo hd de un muro puede tomarse igual a:
donde:
h: es la altura libre de piso,
ρn: es el factor de reducción dependiente del número n de bordes arriostrados, de valor:
- Para un muro arriostrado sólo en cabeza y pie, en general, ρ2 = 1,0. Si se arriostra mediante forjados de hormigón armado con una entrega de al menos 2t/3 y 85 mm, y la excentricidad de la compresión en cabeza es menor de 0,25 t, puede tomarse ρ2 = 0,75.
- Un muro, de espesor t, arriostrado en un sólo borde vertical, con L ≥ 15 t, o en los dos bordes verticales con L ≥ 30 t, se tratará como muro arriostrado sólo en cabeza y pie.
- En los muros arriostrados en cabeza y pie, y en un borde vertical (con el otro borde libre), el valor de ρ3 puede tomarse de las ecuaciones (E.2) y (E.3):
a) para h≤3,5L
ρ3 = ρ2/[1+(ρ2h/(3L))2](E.2)b) para h>3,5L
ρ3 = 1.5·L/h(E.3)siendo:
h: la altura libre del muro
L: la longitud del muro - En los muros arriostrados en los cuatro bordes, el valor de ρ4 puede tomarse de las ecuaciones
(E.4) y (E.5)
a) para h≤1,15L
ρ4 = ρ2/[1+(ρ2h/L)2](E.4)b) para h>1,15L
ρ4 = 0.5·L/h(E.5) - Para un muro libre en cabeza ρ1 = 2,0. Si está arriostrado en algún borde vertical, el valor de ρ será el doble del establecido en las ecuaciones (E.2) a (E.5), según corresponde, para ρ2 = 1,00
5.2.5 Espesor de cálculo de un muro
- El espesor de cálculo, td, de un muro de una hoja, doblado, o de tendel hueco, es el real, o si es preciso descontar rozas o rebajes, el residual.
- Cuando el espesor residual del muro sea menor que la mitad de su espesor real, ese borde se considerará libre a efectos de determinar la altura eficaz.
- En un muro capuchino con ambas hojas enlazadas el espesor eficaz es:
td = [t13+k·t23]1/3(5.14)siendo:
t1, t2: los espesores de las hojas, siendo t1, el de la hoja cargada, tomando t2 no mayor que t1.
k la relación del módulo de elasticidad de la hoja descargada respecto al de la cargada, pero no mayor que 1,0
5.2.6 Esbeltez de un muro
- La esbeltez geométrica, λ, de un muro es la relación: hd/td. Esta relación no será mayor que 27.
5.2.7 Cargas concentradas
- En todo muro que esté solicitado por una carga concentrada,(figura 5.7), la tensión de cálculo alcanzada sobre la superficie de aplicación no será mayor que la resistencia de cálculo del material en el que apoya.
- En un muro realizado con ladrillo macizo siempre que no sea de tendeles huecos, la resistencia de cálculo a compresión de la superficie de aplicación se puede incrementar por un factor ξ. El valor de ξ se toma de la formulación indicada en el Anejo F.
Anejo F. Cálculo del factor de incremento ξ para cargas concentradas
1) El factor de incremento ξ para concentradas se obtiene de la expresión:
ξ = (1+0.15x)·(1.5-1.1·Ab/Aef) ≥ 1(F.1)siendo:
- x = 2·a1/H < 1
- a1: la distancia del borde del área cargada al borde más próximo del muro (figura 5.7),
- H: la altura del muro hasta el nivel en que se aplica la carga,
- Ab: el área cargada, no mayor que 0,45·Aef,
- Aef: el área eficaz del muro (Aef=Lef·t),
- Lef: la longitud de cálculo limitada por una distribución de carga a 60º a media altura del muro, no menor que 2.2·Ab/t,
- t: el espesor del muro, teniendo en cuenta los rehundidos si son mayores de 5mm.
- La excentricidad de la carga en su acometida al muro no será mayor de t/4.
- Además debe comprobarse la compresión repartida en la longitud eficaz Lef incluyendo el efecto de cualquier otra carga vertical, particularmente cuando inciden cargas concentradas próximas, que solapan sus longitudes eficaces, adoptando las medidas que procedan para garantizar el equilibrio.
- La carga concentrada se apoyará sobre piezas u otro material macizo en una longitud igual a la del área cargada incrementada en una longitud adicional al efecto de que las tensiones, suponiendo que se reparten con un ángulo de 60º, sean soportables para el material que constituye el muro.
2) El valor superior de ξ será el menor de 1.25+a1/(2·H) ó 1,5
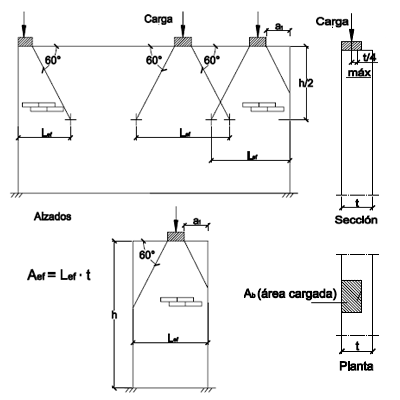
Figura 5.7 Muros con cargas concentradas.
5.3 Muros sometidos a cortante
5.3.2 Capacidad portante
El esfuerzo cortante de cálculo aplicado, VSd, será menor o igual que el esfuerzo cortante resistente, VRd, es decir:
VSd ≤ VRd(5.16)Se considerará la combinación del esfuerzo normal y del esfuerzo cortante más desfavorable de las siguientes:
a) En el muro, el esfuerzo normal, por efecto de las cargas verticales, aplicado con la excentricidad debida a la flexión que causan las acciones horizontales
c) En el muro, el esfuerzo cortante horizontalLa capacidad resistente de cálculo a esfuerzo cortante vale:
VRd = VRd1(5.17)donde
VRd1 = fvd·t·Ld(5.18)siendofvd: la resistencia de cálculo a cortante de la fábrica
t el espesor del muro
Ld la longitud comprimida del muro debida a las acciones verticales, equilibrando a las horizontales, descontando pues la zona de tracción, suponiendo una distribución lineal de tensiones. (Nota: en la aplicación se considera Ld = Longitud del muro).En cualquier caso, la capacidad resistente a cortante no puede ser superior a:
VRd ≤ 2.0 N/mm2·t·Ld(5.20)




