6.1 Flexión simple o compuesta

(1)P Este capítulo se aplica a regiones sin distorsión de las vigas, placas y tipos de elementos para los cuales las secciones se mantienen aproximadamente planas antes y después de aplicar la carga. Las regiones de discontinuidad de vigas y otros elementos en los cuales las secciones planas no se mantienen planas se pueden proyectar y detallarse conforme al apartado 6.5.

(2)P Para determinar la resistencia del momento último de las secciones transversales de hormigón armado o pretensado, se emplean las siguientes hipótesis:

• las secciones planas permanecen planas;
• el alargamiento en la armadura pasiva adherente o en la armadura activa adherente es la misma que la del hormigón circundante, tanto en tracción como en comprensión;
• se desprecia la resistencia a tracción del hormigón;
• las tensiones en el hormigón en compresión se derivan de la relación de cálculo tensión-deformación indicada en el apartado 3.1.7;
• las tensiones en la armadura activa y pasiva se derivan de las curvas de cálculo de la figura 3.8 del apartado 3.2 y la figura 3.10 del apartado 3.3;
• el alargamiento inicial en las armaduras activas se considera al evaluar sus tensiones.

(3)P La deformación unitaria por compresión en el hormigón se debe limitar a ε_cu2, o ε_cu3, dependiendo del diagrama utilizado de tensión-deformación, véase el apartado 3.1.7 y la tabla 3.1. Los alargamientos en la armadura pasiva y en el acero de pretensado se deben limitar a ε_ud (donde se pueda aplicar); véase el punto (2) del apartado 3.2.7 y el punto (7) del apartado 3.3.6, respectivamente.

(4) Para secciones transversales con armadura simétrica cargada mediante la fuerza de compresión es necesario suponer la excentricidad mínima, e_o = h/30 no menor que 20 mm, donde h es el canto de la sección.

5) En partes de secciones transversales sometidas a una carga aproximadamente concéntrica (e_d/h ≤ 0,1), tales como cabezas comprimidas de vigas en cajón, la deformación unitaria por compresión media en esa parte de la sección se debería limitar a ε_c2 (o ε_c3 si se utiliza la relación bilineal de la figura 3.4).

(6) El posible rango de distribuciones de deformación unitaria se muestra en la figura 6.1.

(7) Para elementos pretensados con armaduras activas no adherentes de modo permanente véase el apartado 5.10.8.

(8) Para armaduras activas externas el alargamiento en la armadura activa entre dos puntos de contacto subsiguiente (anclajes o sillas de desviación) se supone constante. El alargamiento en las armaduras activas es por lo tanto igual al alargamiento inicial, obtenido justo después de que se haya producido la operación de pretensado, aumentado por el alargamiento resultante de la deformación estructural entre las zonas de contacto consideradas. Véase también el apartado 5.10.

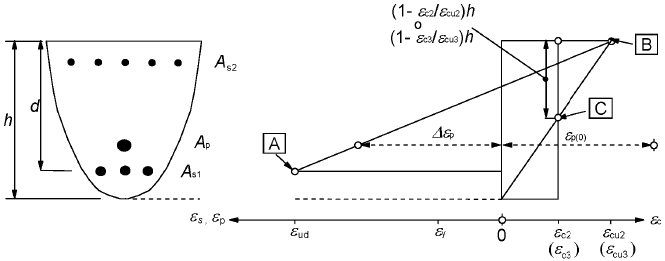
A - Límite de alargamiento por tracción de la armadura pasiva
B - Límite de deformación unitaria del hormigón a compresión
C - Límite de deformación unitaria del hormigón a compresión pura

Figura 6.1: Distribuciones posibles del alargamiento y de la deformación unitaria en estado límite último

---

3.1 Hormigón
3.1.7 Relación entre tensión-deformación para el cálculo de secciones transversales

(2) Se pueden usar otras relaciones tensión-deformación simplificadas si son equivalentes a la definida en el punto (1) o quedan del lado de la seguridad, por ejemplo la relación bilineal conforme a la figura 3.4 (la tensión de compresión y la deformación unitaria de acortamiento se muestran en valores absolutos) con valores de ε_c3 y ε_cu3 conforme a la tabla 3.1.

ε_c3(⁰/₀₀) = 1.75 para f_ck ≤ 50 MPa
ε_c3(⁰/₀₀) = 1,75 + 0,55[(f_ck - 50)/40] para 50 < f_ck ≤ 90 MPa

y

ε_cu3(⁰/₀₀) = 3.50 para f_ck ≤ 50 MPa
ε_cu3(⁰/₀₀) = 2.6 + 35[(90 - f_ck)/100]⁴ para 50 < f_ck ≤ 90 MPa

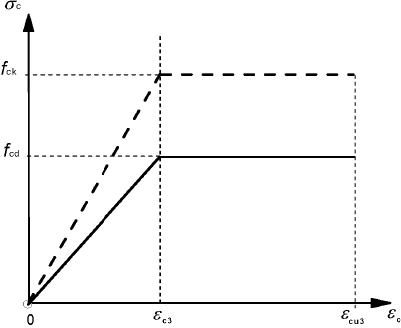
Figura 3.4 - Diagrama bilineal tensión-deformación

(3) Se puede suponer una distribución rectangular de tensiones como se indica en la figura 3.5. El coeficiente λ, que define la profundidad eficaz de la zona de compresión y el coeficiente η, que define la resistencia eficaz, se obtiene de:

y

NOTA: Si la anchura de la zona de compresión disminuye en la dirección de la fibra de compresión extrema, el valor η·f_cd se debería reducir un 10%.

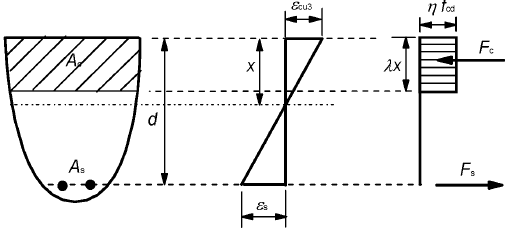
Figura 3.5 - Diagrama rectangular de la tensión

3.2 Armaduras pasivas
3.2.7 Hipótesis de cálculo

(2) Para un cálculo normal, se puede emplear cualquiera de las siguientes hipótesis (véase la figura 3.8):

• a) una rama superior inclinada con un límite de alargamiento de ε_ud y una tensión máxima de k·f_yk/γ_s, donde k= (f_t/f_y)_k;

NOTA 1 El valor de ε_ud para uso en España es

• Se adopta, con carácter general, ε_ud = 0.90·ε_uk
  Cuando el Autor del proyecto estime que las armaduras poseen un nivel de garantía suficiente, puede considerar un valor ε_ud = ε_uk
• En cualquier caso, se adoptará una deformación unitaria de las armaduras pasivas en el cálculo que no sea superior al 10‰.

NOTA 2 El valor de (f_t/f_y)_k se indica en la tabla C1:

Tabla C.1 − Propiedades del acero para armar

	Barras y redondos desenrollados
Clase	A	B	C
Límite elástico característico fyk ó f0,2k (MPa)	400 a 600
Valor mínimo de k = (ft/fy)k	≥ 1,05	≥ 1,08	≥ 1,15
Deformación unitaria característica máxima, εuk (%)	≥ 2,5	≥ 5,0	≥ 7,5

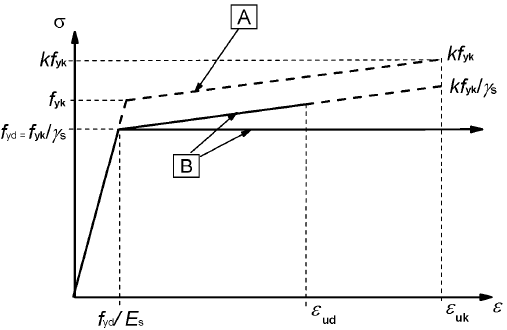
A- Idealizado; B- Cálculo
Figura 3.8 - Diagramas idealizados y de cálculo de tensión-deformación para acero de armaduras pasivas (para tracción y compresión)

(3) Se puede aceptar que el valor medio de la densidad es 7850 kg/m³.

(4) Se puede suponer que el valor de cálculo del módulo de elasticidad es, Es, 200 GPa.

---

Dominios de deformación

Las deformaciones límite de las secciones, según la naturaleza de la solicitación, conducen a admitir los siguientes dominios:

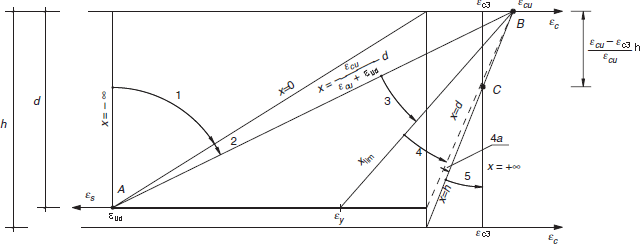
• Dominio 1: Tracción simple o compuesta en donde toda la sección está en tracción. Las rectas de deformación giran alrededor del punto A correspondiente a un alargamiento de la armadura más traccionada de ε_ud.
• Dominio 2: Flexión simple o compuesta en donde el hormigón no alcanza la deformación de rotura por flexión ε_cu3. Las rectas de deformación giran alrededor del punto A.
• Dominio 3: Flexión simple o compuesta en donde las rectas de deformación giran alrededor del punto B correspondiente a la deformación de rotura por flexión del hormigón ε_cu3 definida en el apartado 3.1.7. El alargamiento de la armadura más traccionada está comprendido entre ε_ud y ε_y, siendo ε_y, el alargamiento correspondiente al límite elástico del acero.
• Dominio 4: Flexión simple o compuesta en donde las rectas de deformación giran alrededor del punto B. El alargamiento de la armadura más traccionada está comprendido entre ε_y y 0.
• Dominio 4a: Flexión compuesta en donde todas las armaduras están comprimidas y existe una pequeña zona de hormigón en tracción. Las rectas de deformación giran alrededor del punto B.
• Dominio 5: Compresión simple o compuesta en donde ambos materiales trabajan a compresión. Las rectas de deformación giran alrededor del punto C definido por la recta correspondiente a la deformación de rotura del hormigón por compresión, ε_c3, definido en el apartado 3.1.7.

Se denomina eje neutro de una sección a la recta de deformación nula. Su distancia a la fibra más comprimida se designa por "x".

La variación de el eje neutro desde - ∞ hasta + ∞ , determina todas las combinaciones posibles de momento flector y esfuerzo axil últimos en la sección.

Comprobación de secciones rectangulares

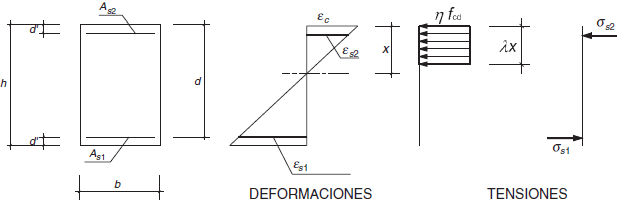
Las ecuaciones de equilibrio que determinan el momento y axil últimos en la sección (Mu and Nu) son las siguientes:
(Diagrama de interacción axil-momento)

Dominio 1:

- ∞ < x ≤ 0

• N_u(x) = - A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u (x)= - A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(d'-x)/(d-x)

Dominio 2:

0 < x ≤ d · ε_cu/(ε_cu+ε_ud)

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u(x)= η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(x-d')/(d-x)

Dominio 3:

d · ε_cu/(ε_cu+ε_ud) < x ≤ x_lim

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Dominio 4:

x_lim< x ≤ d

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Dominio 4a:

d < x ≤ h

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u/x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(x-d)/x

Dominio 5:

h < x < ∞

• N_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b·[h/2-[1- (1-λ)·h/x]·h/2] + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_c3·(x-d')/(x-h/2)
• ε_s1(x) = ε_c3·(x-d)/(x-h/2)