EC2: Anchorage of longitudinal reinforcement

8.4 Anchorage of longitudinal reinforcement

8.4.1 General

(1)P Reinforcing bars, wires or welded mesh fabrics shall be so anchored that the bond forces are safely transited to the concrete avoiding longitudinal cracking or spalling. Transverse reinforcement shall be provided if necessary.

(2) Methods of anchorage are shown in Figure 8.1

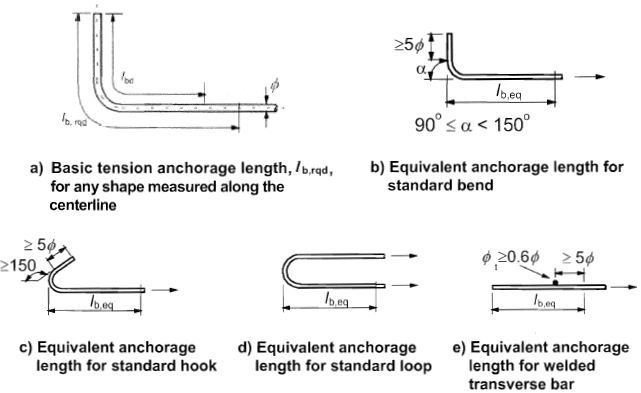
Figure 8.1: Methods of anchorage other than by a straight bar

(3) Bends and hooks do not contribute to compression anchorages

(4) Concrete failure inside bends should be prevented by complying with 8.3 (3).

(5) Where mechanical devices are used the test requirements should be in accordance with the relevant product standard or a European Technical Approval.

8.4.2 Ultimate bond stress

(1)P The ultimate bond strength shall be sufficient to prevent bond failure.

(2) The design value of the ultimate bond stress, f_bd, for ribbed bars may be taken as:

f_bd = 2.25 · η₁ · η₂ · f_ctd

(8.2)

where:

- f_ctd is the design value of concrete tensile strength according to 3.1.6 (2)P. Due to the increasing brittleness of higher strength concrete, f_ctk,0.05 should be limited here to the value for C60/75, unless it can be verified that the average bond strength increases above this limit.

3.1.6 (2)P The value of the design tensile strength, fctd is defined as

f_ctd = α_ct · f_ctk,0.05 / γ_c

γ_c is the partial safety factor for concrete = 1.5 (situation Persistent and Transient)

α_ct is a coefficient taking account of long term effects on the tensile strength and of unfavorable effects, resulting from the way the load is applied.

Note: The value of α_ct for use in a Country may be found in its National Annex. The recommended value is 1.0.

Table 3.1: f_{ctk ,0.05} = 0.7 · f_ctm ; f_ctm = 0.3 · f_ck ^(2/3) (f_ck ≤ 50 MPa)

- η₁ is a coefficient related to the quality of the bond condition and the position of the bar during concreting (see Figure 8.2):

η₁ = 1.0 when 'good' conditions are obtained and
η₁ = 0.7 for all other cases and for bars in structural elements built with slip-forms, unless it can be shown that 'good' bond conditions exist

- η₂ is related to the bar diameter:

η₂ = 1.0 for φ ≤ 32 mm
η₂ = (132 - φ)/100 for φ > 32 mm

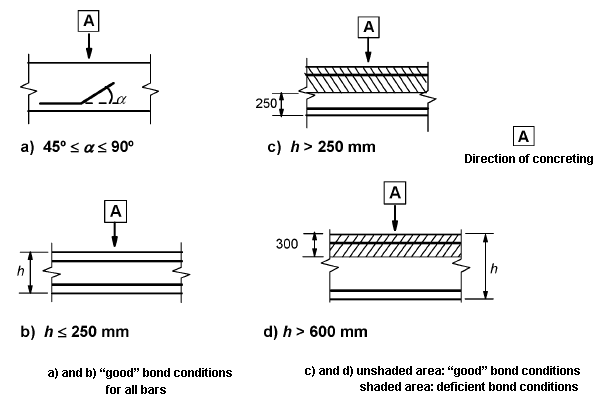
Figure 8.2: Description of bond conditions

8.4.3 Basic anchorage length

(1)P The calculation of the required anchorage length shall take into consideration the type of steel and bond properties of the bars.

(2) The basic required anchorage length, l_b,rqd, for anchoring the force A_s·σ_sd in a straight bar assuming constant bond stress equal to f_bd follows from:

l_b,rqd = (Φ / 4) (σ_sd / f_bd)

(8.3)

Where σ_sd is the design stress of the bar at the position from where the anchorage is measured from.
Values for f_bd are given in 8.4.2.

(3) For bent bars the basic required anchorage length, l_b,rqd, and the design length, l_bd, should be measured along the centre-line of the bar (see Figure 8.1 a).

8.4.4 Design anchorage length

(1) The design anchorage length, l_bd, is:

l_bd = α₁α₂α₃α₄α₅ · l_b,rqd ≥ l_b,min

(8.4)

where α₁ , α₂ , α₃, α₄ and α₅ are coefficients given in Table 8.2:

α₁ is for the effect of the form of the bars assuming adequate cover (see Figure 8.1).

α₂ is for the effect of concrete minimum cover (see Figure 8.3)

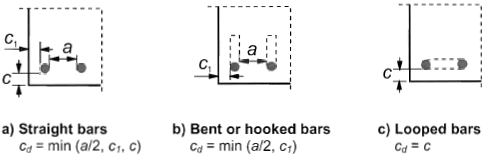
Figure 8.3: Values of Cd for beams and slabs

α₃ is for the effect of confinement by transverse reinforcement

α₄ is for the influence of one or more welded transverse bars (Φt > 0.6Φ) along the design anchorage length l_bd (see also 8.6)

α₅ is for the effect of the pressure transverse to the plane of splitting along the design anchorage length

The product (α2·α3·α5) ≥ 0.7

(8.5)

l_b,rqd is taken from Expression (8.3)

l_b,min is the minimum anchorage length if no other limitation is applied:

- for anchorages in tension: Ib,min ≥ max{0,3·lb,rqd; 10·φ; 100 mm}

(8.6)

- for anchorages in compression: Ib,min ≥ max{0,6·lb,rqd; 10·φ; 100 mm}

(8.7)

(2) As a simplified alternative to 8.4.4 (1) the tension anchorage of certain shapes shown in Figure 8.1 may be provided as an equivalent anchorage length, l_b,eq. l_b,eq is defined in this figure and may be taken as:

- α₁·l_b,rqd for shapes shown in Figure 8.1 b to 8.1 d (see Table 8.2 for values of α₁)
- α₄·l_b,rqd for shapes shown in Figure 8.1 e (see Table 8.2 for values of α₄).

where

α₁ and α₄ are defined in (1)
l_b,rqd is calculated from Expression (8.3)

Table 8.2: Values of α₁, α₂, α₃, α₄ and α₅ coefficients

Influencing factor	Type of anchorage	Reinforcement bar
Influencing factor	Type of anchorage	In tension	In compression
Shape of bars	Straight	α₁ = 1	α₁ = 1
Shape of bars	Other than straight see Figure 8.1 (b), (c) and (d)	α₁ = 0.7 if Cd >3φ otherwise α₁ = 1 (see Figure 8.3 for values of Cd)	α₁ = 1
Concrete cover	Straight	α₂ = 1-0.15 (Cd - φ)/ φ ≥ 0.7 and ≤ 1.0	α₂ = 1
Concrete cover	Other than straight (see Figure 8.1 (b), (c) and (d)	α₂ = 1-0, 15 (Cd - 3φ)/ φ ≥ 0.7 and ≤ 1.0 (see Figure 8.3 for values of Cd)	α₂ = 1
Confinement by transverse reinforcement not welded to main reinforcement	All types	α₃ = 1 - Kλ ≥ 0.7 and ≤ 1.0	α₃ = 1
Confinement by welded transverse reinforcement	All types, position and size as specified in Figure 8.1 e	α₄ = 0.7	α₄ = 0.7
Confinement by transverse pressure	All types	α₅ = 1 - 0.04p ≥ 0.7 and ≤ 1.0	--
where: λ = (∑A_st - ∑A_st,min) / A_s ∑A_st: cross-sectional area of the transverse reinforcement along the design anchorage length l_bd ∑A_st,min: cross-sectional area of the minimum transverse reinforcement = 0,25 As for beams and 0 for slabs. As: area of a single anchored bar with maximum bar diameter K: values shown in Figure 8.4 p: transverse pressure [MPa] at ultimate limit state along l_bd

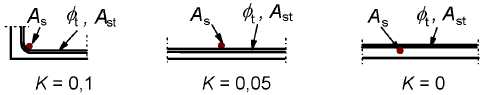
Figura 8.4
Figure 8.4: Values of K for beams and slabs