EC2: Section minimale des armatures
7.3.2 Sections minimales d'armatures
(1)P Si la maîtrise de la fissuration est requise, une quantité minimale d'armatures adhérentes est nécessaire pour maîtriser la fissuration dans les zones où l'on prévoit l'existence de contraintes de traction. Cette quantité peut être estimée à partir de l'équilibre entre les efforts de traction dans le béton juste avant la fissuration et les efforts de traction dans les armatures à la limite d'élasticité ou le cas échéant à une contrainte inférieure pour limiter l'ouverture des fissures.
(2) À moins qu'un calcul plus rigoureux ne démontre qu'une section réduite suffit, les sections minimales d'armatures peuvent être calculées comme indiqué ci-après. Dans le cas des sections profilées telles que poutres en T et poutres-caissons, il convient de déterminer séparément le ferraillage minimal pour les différentes parties de la section (membrures et âmes).
où :
- As,min est la section minimale d'armatures de béton armé dans la zone tendue
- Act est l'aire de la section droite de béton tendu. La zone de béton tendue est la partie de la section dont le calcul montre qu'elle est tendue juste avant la formation de la première fissure
- σs est la valeur absolue de la contrainte maximale admise dans l'armature immédiatement après la formation de la fissure. Elle peut être prise égale à la limite d'élasticité, fyk, de l'armature. Une valeur inférieure peut toutefois être adoptée afin de satisfaire les limites d'ouverture de fissures en fonction du diamètre maximal ou de l'espacement maximal des barres (voir 7.3.3 (2))
- fct,eff est la valeur moyenne de la résistance en traction du béton au moment où les premières fissures sont supposées apparaître :
fct,eff = fctm toutefois on peut adopter une valeur inférieure, (fctm(t)), si l'on prévoit que la fissuration se produira avant 28 jours - k est un coefficient qui tient compte de l'effet des contraintes non-uniformes auto-équilibrées conduisant à une réduction des efforts dus aux déformations gênées :
= 1,0 pour les âmes telles que h ≤ 300 mm ou les membrures d'une largeur inférieure à 300 mm
= 0,65 pour les âmes telles que h ≥ 800 mm ou les membrures d'une largeur supérieure à 800 mm
les valeurs intermédiaires peuvent être obtenues par interpolation - kc est un coefficient qui tient compte de la répartition des contraintes dans la section immédiatement avant la fissuration ainsi que de la modification du bras de levier :
En traction pure : kc = 1,0
En flexion simple ou en flexion composée :
- sections rectangulaires et âmes des caissons et des sections en T:
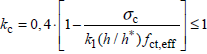 (7.2)
(7.2)
- membrures des caissons et des sections en T :
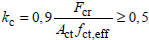 (7.3)
(7.3)
avec- σc contrainte moyenne dans le béton régnant dans la partie de la section considérée :
σc = NEd / (bh)(7.4) - NEd effort normal agissant à l'état-limite de service dans la partie de la section considérée (positif pour un effort de compression). Il convient de déterminer NEd en considérant les valeurs caractéristiques de la précontrainte et de l'effort normal sous la combinaison d'actions appropriée
- h* = h pour h < 1,0 m
h* = 1,0 m pour h ≥ 1,0 m - k1 est un coefficient qui prend en compte les effets de l'effort normal sur la répartition des contraintes :
k1 = 1,5 si NEd est un effort de compression
k1= 2h*/(3h) si NEd est un effort de traction - Fcr est la valeur absolue de l'effort de traction dans la membrure juste avant la fissuration, du fait du moment de fissuration calculé avec fct,eff
- σc contrainte moyenne dans le béton régnant dans la partie de la section considérée :
9.2 Poutres
9.2.1 Armatures longitudinales
9.2.1.1 Sections minimale et maximale d'armatures
(1) Il convient que la section d'armatures longitudinales tendues ne soit pas inférieure à As,min.
NOTE 1 Voir également 7.3 pour la section d'armatures longitudinale tendues permettant la maîtrise de la fissuration
NOTE 2 La valeur de As,min à utiliser en France est comme suit :
où :
- bt désigne la largeur moyenne de la zone tendue ; pour une poutre en T dont la membrure supérieure est comprimée, seule la largeur de l'âme est prise en compte dans le calcul de bt
- fctm Il convient de déterminer fctm en fonction de la classe de résistance appropriée, conformément au Tableau 3.1.
fctm = 0,30 × fck(2/3), fck ≤ 50
fctm = 2.12·Ln(1+(fcm/10)), fck > 50/60
avec fcm = fck+8 (MPa)
(2) Il convient de considérer les sections contenant une quantité d'armatures inférieures à As,min comme des sections non armées.
(3) Il convient que la section des armatures tendues ou comprimées n'excède pas As,max en dehors des zones de recouvrement.
NOTE La valeur de As,max à utiliser en France est 0.04·Ac.
9.3 Dalles pleines
(1) La présente clause s'applique aux dalles pleines uni-directionnelles et bi-directionnelles pour lesquelles b et leff ne sont pas inférieures à 5h.
9.3.1 Armatures de flexion
9.3.1.1 Généralités
(1) Pour le pourcentage d'acier minimal et le pourcentage d'acier maximal dans la direction principale, 9.2.1.1 (1) et (3) s'appliquent.
(2) Il convient de prévoir, dans les dalles uni-directionnelles, des armatures transversales secondaires représentant au moins 20 % des armatures principales. Au voisinage des appuis, des armatures transversales aux barres principales supérieures ne sont pas nécessaires lorsqu'il n'existe aucun moment fléchissant transversal.
(3) Il convient que l'espacement des barres ne soit pas supérieur smax,slabs.
NOTE La valeur de smax,slabs à utiliser en France est comme suit :
- pour les armatures principales, smax,slabs = 3·h ≤ 400 mm, woù h est l'épaisseur totale de la dalle ;
- pour les armatures secondaires, smax,slabs = 3.5·h ≤ 450 mm
Dans les zones sollicitées par des charges concentrées ou dans les zones de moment maximal, ces dispositions deviennent respectivement :
- pour les armatures principales, smax,slabs = 2·h ≤ 250 mm
- pour les armatures secondaires, smax,slabs = 3·h ≤ 400 mm.
9.5 Poteaux
9.5.1 Généralités
(1) La présente clause traite des poteaux pour lesquels la plus grande dimension h est inférieure ou égale à 4 fois la plus petite dimension b.
9.5.2 Armatures longitudinales
(1) Il convient que le diamètre des barres longitudinales ne soit pas inférieur à Φmin.
NOTE La valeur de Φmin à utiliser en France est 8 mm.
(2) Il convient que la quantité totale d'armatures longitudinales ne soit pas inférieure à As,min
NOTE La valeur de As,min à utiliser en France est comme suit :
où :
- fyd est la limite d'élasticité de calcul des armatures
- NEd est l'effort normal agissant de compression.
(3) Il convient de limiter l'aire de la section des armatures longitudinales à As,max
NOTE La valeur de As,max à utiliser en France est comme suit :
- As,max = 0,04·Ac hors des zones de recouvrement, à moins que l'on puisse prouver que l'intégrité du béton n'est pas affectée et que la pleine résistance est obtenue aux ELU. Au droit des recouvrements, il convient d'augmenter cette limite jusqu' à 0,08·Ac.
(4) Pour des poteaux de section polygonale, il convient de disposer au moins une barre dans chaque angle. Dans un poteau circulaire, il convient que le nombre de barres longitudinales ne soit pas inférieur à quatre.
9.6 Voiles
9.6.1 Généralités
(1) La présente clause se rapporte aux voiles en béton armé dont la longueur est au moins égale à 4 fois l'épaisseur et dont les armatures sont prises en compte dans le calcul de la résistance. Pour les voiles soumis principalement à une flexion due à des charges non-coplanaires, les règles pour les dalles s'appliquent (voir 9.3).
9.6.2 Armatures verticales
(1) Il convient que l'aire de la section des armatures verticales soit comprise entre As,vmin et As,vmax.
NOTE 1. La valeur de As,vmin à utiliser en France est comme suit :
- As,vmin = 0.002·Ac
- pour les bâtiments la valeur à utiliser est la suivante :
As,vmin = 0 si NEd ≤ NRd,12
As,vmin = 0.001·Ac·(1+2·(NEd-NRd,12)/NRd,6-NRd,12)) si NEd > NRd,12
avec :
- NRd,6 est la valeur de calcul de l'effort normal résistant de ce voile ou de cette bande de voile, calculé selon la Section 6 ;
- NRd,12 est la valeur de calcul de l'effort normal résistant de ce voile ou de cette bande de voile, calculé selon la Section 12.
NRd,12 = η·fcd · b · hw · (1 – 2e/hw)
où :
η·fcd est la résistance de calcul effective en compression
b est la largeur totale de la section droite
hw est la hauteur totale de la section droite
e est l'excentricité de NEd dans la direction hw.
NOTE 2 La valeur de As,vmax à utiliser en France est 0.04·Ac
(2) Lorsque le calcul conduit à prévoir l'aire minimale d'armatures, As,vmin, il convient de disposer la moitié de cette aire sur chaque face.
(3) Il convient de limiter la distance entre deux barres verticales adjacentes à 3 fois l'épaisseur du voile ou à 400 mm si cette valeur est inférieure.
9.6.3 Armatures horizontales
(1) Il convient de prévoir des armatures horizontales parallèles aux parements du voile (et aux bords libres) sur chaque face. Il convient que l'aire de la section de ces armatures ne soit pas inférieure à As,hmin.
NOTE 1. La valeur de As,hmin à utiliser en France est comme suit :
- As,hmin = max (0.25·As,vmin, 0.001·Ac)
- pour les bâtiments avec NEd ≤ NRd,12, As,hmin = 0
(2) Il convient de limiter à 400 mm l'espacement entre deux barres horizontales adjacentes.
9.8 Fondations
9.8.1 Semelles de fondation de poteaux ou de voiles
(1) Il convient de respecter un diamètre minimal d'armatures Φmin
NOTE La valeur de Φmin à utiliser en France est 8 mm.





Commentaires
La bonne humeur est un bon
La bonne humeur est un bon compagnon de voyage. Voilà mon expression à propos de cet application