EC2: Calcul de la résistance à flexion
6.1 Flexion simple et flexion composée
(1)P La présente section s'applique aux régions sans discontinuité des poutres, dalles et autres éléments analogues dont les sections demeurent approximativement planes avant et après le chargement. Le dimensionnement et le choix des dispositions constructives des régions de discontinuité des poutres et autres éléments, dans lesquelles les sections planes ne restent pas planes, peuvent être effectués conformément à 6.5.
(2)P La détermination du moment résistant ultime de sections droites de béton armé ou de béton précontraint s'appuie sur les hypothèses suivantes :
- les sections planes restent planes
- les armatures adhérentes (armatures de béton armé ou armatures de précontrainte), qu'elles soient tendues ou comprimées, subissent les mêmes déformations relatives que le béton adjacent
- la résistance en traction du béton est négligée
- les contraintes dans le béton comprimé se déduisent du diagramme contrainte-déformation de calcul donné en 3.1.7
- les contraintes dans les armatures de béton armé ou dans les armatures de précontrainte se déduisent des diagrammes de calcul donnés en 3.2 (Figure 3.8) et en 3.3 (Figure 3.10)
- l'évaluation des contraintes dans les armatures de précontrainte tient compte de leur déformation relative initiale.
(3)P La déformation en compression du béton doit être limitée à εcu2, ou εcu3, selon le diagramme contrainte-déformation utilisé — voir 3.1.7 et Tableau 3.1. Les déformations des armatures de béton armé et des armatures de précontrainte doivent être limitées à εud si cette limite existe; voir 3.2.7 (2) et 3.3.6 (7) respectivement.
(4) Dans le cas de sections droites avec un ferraillage symétrique, soumises à un effort de compression, il convient d'adopter une excentricité minimale eo = h/30, ou 20 mm si cette valeur est supérieure, h étant la hauteur de la section.
5) Dans les parties des sections qui sont soumises à une charge approximativement centrée (ed/h ≤ 0,1), telles que les membrures comprimées des poutres-caissons, il convient de limiter la déformation moyenne en compression dans cette partie de la section à εc2 (ou εc3 si l'on utilise la relation bilinéaire de la Figure 3.4).
(6) La Figure 6.1 montre les valeurs limites des déformations relatives admissibles.
(7) Pour des éléments précontraints, avec des armatures de précontrainte non-adhérentes de manière permanente, voir 5.10.8.
(8) Dans le cas des armatures de précontrainte extérieures, on admet que la déformation de l'armature entre deux points de contact consécutifs (ancrages ou selles de déviation) est constante. La déformation de l'armature est alors égale à la déformation relative initiale, obtenue immédiatement après l'achèvement de la mise en tension, majorée de la déformation résultant des déformations de la structure entre les zones de contact considérées. Voir également 5.10.
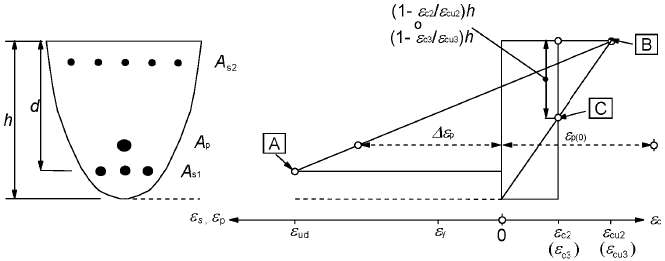
A - Limite de déformation relative en traction des armatures de béton armé
B - Limite de déformation relative du béton en compression
C - Limite de déformation relative du béton en compression pure
Figure 6.1 : Diagramme des déformations relatives admissibles à l'état-limite ultime
3.1 Béton
3.1.7 Relations contrainte-déformation pour le calcul des sections
(2) D'autres relations contrainte-déformation simplifiées sont admises, à condition qu'elles soient équivalentes, voire plus conservatrices, que celle définie en (1) — diagramme bilinéaire de la Figure 3.4, par exemple (contrainte de compression et raccourcissement représentés en valeur absolue), avec les valeurs de εc3 y εcu3 telles qu'indiquées dans le Tableau 3.1.
εc3(0/00) = 1.75 pour fck ≤ 50 MPa
εc3(0/00) = 1,75 + 0,55[(fck - 50)/40] pour 50 < fck ≤ 90 MPa
et
εcu3(0/00) = 3.50 pour fck ≤ 50 MPa
εcu3(0/00) = 2.6 + 35[(90 - fck)/100]4 pour 50 < fck ≤ 90 MPa
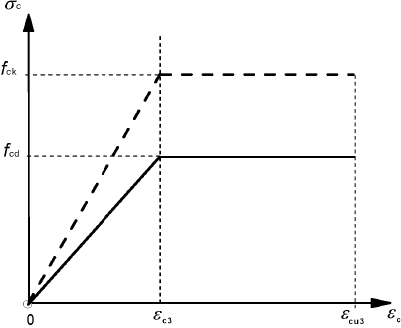
Figure 3.4 : Diagramme bilinéaire
(3) On peut admettre un diagramme rectangulaire de compression dans le béton (tel que représenté sur la Figure 3.5). Le coefficient λ, définissant la hauteur utile de la zone comprimée, et le coefficient η, définissant la résistance effective, valent :
et
NOTE Si la largeur de la zone comprimée diminue dans la direction de la fibre extrême la plus comprimée, il convient de réduire η·fcd de 10%.
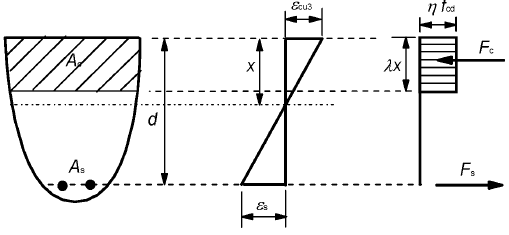
Figure 3.5 : Diagramme rectangulaire
3.2 Acier de béton armé
3.2.7 Hypothèses de calcul
(2) Pour un calcul courant, l'une ou l'autre des hypothèses suivantes peut être faite (voir Figure 3.8) :
- a) branche supérieure inclinée, avec une limite de déformation égale à εud et une contrainte maximale k·fyk/γs pour εuk, avec k= (ft/fy)k;
NOTE 1 La valeur de εud à utiliser en France est :
- εud = 0.90·εuk
NOTE 2 La valeur de (ft/fy)k est donnée dans le Tableau C.1 (Annexe C):
Tableau C.1 : Propriétés des armatures
| Barres et fils redressés | |||
| Classe | A | B | C |
| Limite caractéristique d'élasticité fyk ou f0,2k (MPa) | 400 à 600 | ||
| Valeur minimale de k = (ft/fy)k | ≥ 1,05 | ≥ 1,08 | ≥ 1,15 |
| Valeur caractéristique de la déformation relative sous charge maximale, εuk (%) | ≥ 2,5 | ≥ 5,0 | ≥ 7,5 |
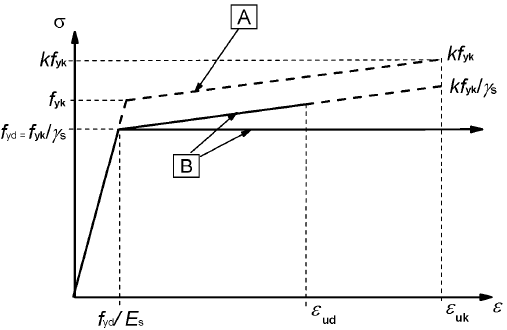
A- Diagramme simplifié; B- Diagramme de calcul
Figure 3.8 : Diagramme contrainte-déformation simplifié et diagramme de calcul pour les aciers de béton armé (tendus ou comprimés)
(3) La valeur moyenne de la masse volumique peut être supposée égale à 7850 kg/m3.
(4) La valeur de calcul du module d'élasticité Es peut être supposée égale à 200 GPa.
Diagrammes des déformations ou des 3 pivots
Les déformations limites des sections, définis à partir des "3 pivots" A, B et C, permettent reconnaître les domaines suivants :
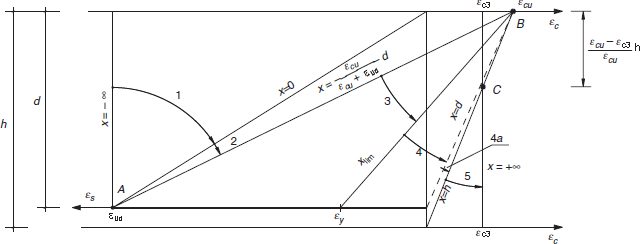
- Domaine 1: Traction pure ou composée où toute la section est en traction. Les lignes de déformation tournent autour du point A correspondant à l'allongement maximal de l'armature plus tendue εud.
- Domaine 2: Flexion simple ou composée où le béton ne atteint pas la déformation maximale en flexion εcu3. Les lignes de déformation tournent autour du point A.
- Domaine 3: Flexion simple ou composée où les lignes de déformation tournent autour du point B correspondant a la déformation maximale en flexion de le béton εcu3 définie en 3.1.7. L'allongement de l'armature plus tendue est compris entre εud et εy, où εy est l'allongement correspondant au limite d'élasticité de l'acier.
- Domaine 4: Flexion simple ou composée où les lignes de déformation tournent autour du point B. L'allongement de l'armature plus tendue est compris entre εy et 0.
- Domaine 4a: Flexion composée où toutes les armatures sont compressées et il y a une petite zone de béton en traction. Les lignes de déformation tournent autour du point B.
- Domaine 5: Compression pure ou composée en où les deux matériaux travaillent en compression. Les lignes de déformation tournent autour du point C correspondant à la déformation maximale du béton en compression, εc3, définie en 3.1.7.
Il est appelé l'axe neutre d'une section à la ligne de déformation nulle. Sa distance a la fibre plus compressée est désigné par "x".
La variation de l'axe neutre de - ∞ a + ∞ , détermine toutes les combinaisons possibles de moment de flexion et force axiale ultimes de la section.
Vérification des sections rectangulaires
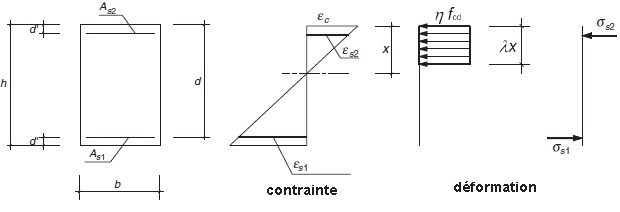
Les équations d'équilibre qui déterminent le moment de flexion et la force axiale ultimes de la section (Mu et Nu) sont les suivantes :
(Diagramme d'interaction)
Domaine 1:
- ∞ < x ≤ 0
- Nu(x) = - As2·σs2[εs2] - As1·k·fyd
- Mu (x)= - As2·σs2[εs2]·(h/2-d') - As1·k·fyd·(h/2-d)
- εs2(x) = εud·(d'-x)/(d-x)
Domaine 2:
0 < x ≤ d · εcu/(εcu+εud)
- Nu(x) = η·fcd·λ·x·b + As2·σs2[εs2] - As1·k·fyd
- Mu(x)= η·fcd·λ·x·b·(h/2-λ·x/2) + As2·σs2[εs2]·(h/2-d') - As1·k·fyd·(h/2-d)
- εs2(x) = εud·(x-d')/(d-x)
Domaine 3:
d · εcu/(εcu+εud) < x ≤ xlim
- Nu(x) = η·fcd·λ·x·b + As2·σs2[εs2] - As1·σs1[εs1]
- Mu(x) = η·fcd·λ·x·b·(h/2-λ·x/2) + As2·σs2[εs2]·(h/2-d') - As1·σs1[εs1]·(h/2-d)
- εs2(x) = εcu·(x-d')/x
- εs1(x) = εcu·(d-x)/x
Domaine 4:
xlim< x ≤ d
- Nu(x) = η·fcd·λ·x·b + As2·σs2[εs2] - As1·σs1[εs1]
- Mu(x) = η·fcd·λ·x·b·(h/2-λ·x/2) + As2·σs2[εs2]·(h/2-d') - As1·σs1[εs1]·(h/2-d)
- εs2(x) = εcu·(x-d')/x
- εs1(x) = εcu·(d-x)/x
Domaine 4a:
d < x ≤ h
- Nu(x) = η·fcd·λ·x·b + As2·σs2[εs2] + As1·σs1[εs1]
- Mu/x) = η·fcd·λ·x·b·(h/2-λ·x/2) + As2·σs2[εs2]·(h/2-d') + As1·σs1[εs1]·(h/2-d)
- εs2(x) = εcu·(x-d')/x
- εs1(x) = εcu·(x-d)/x
Domaine 5:
h < x < ∞
- Nu(x) = η·fcd·[1- (1-λ)·h/x]·h·b + As2·σs2[εs2] + As1·σs1[εs1]
- Mu(x) = η·fcd·[1- (1-λ)·h/x]·h·b·[h/2-[1- (1-λ)·h/x]·h/2] + As2·σs2[εs2]·(h/2-d') + As1·σs1[εs1]·(h/2-d)
- εs2(x) = εc3·(x-d')/(x-h/2)
- εs1(x) = εc3·(x-d)/(x-h/2)





Commentaires
Je tiens à vous féliciter
Je tiens à vous féliciter pour la qualité de votre outil qui produit des résultats conformes à mes attentes.
j’ai deux questions concernant la résolution du système d’équations non linéaires utilisé par votre application :
- La méthode de résolution employée garantit-elle une convergence systématique ?
- J’ai remarqué que le programme calcule parfois Mu et d’autres fois -Mu, même lorsque Md est supérieur à zéro. Pourriez-vous m’expliquer pourquoi ?