6.1 Flexão simples e flexão composta

(1)P Esta secção aplica-se às zonas sem descontinuidades de vigas, lajes e outros elementos semelhantes cujas secções se mantêm aproximadamente planas antes e após o carregamento. As zonas de descontinuidade de vigas e de outros elementos nos quais as secções planas não permanecem planas poderão ser calculadas e pormenorizadas de acordo com 6.5.

(2)P A determinação da resistência à flexão última de secções de betão armado ou pré-esforçado baseia-se nas seguintes hipóteses:

• as secções mantêm-se planas;
• a extensão nas armaduras aderentes, em tracção ou em compressão, é a mesma da do betão que as envolve;
• a resistência do betão à tracção é ignorada;
• as tensões no betão comprimido são obtidas do diagrama tensões-extensões de cálculo, indicado em 3.1.7;
• as tensões nas armaduras de betão armado ou nas armaduras de pré-esforço são obtidas dos diagramas de cálculo indicados em 3.2 (ver a Figura 3.8) e 3.3 (ver a Figura 3.10);
• a avaliação das tensões nas armaduras de pré-esforço tem em conta a extensão inicial dessas armaduras.

(3)P A extensão de compressão no betão deve ser limitada a ε_cu2, o ε_cu3, conforme o diagrama tensõesextensões utilizado, ver 3.1.7 e Quadro 3.1. As extensões no aço para betão armado e no aço de pré-esforço devem ser limitadas a ε_ud (caso exista); ver 3.2.7(2) e 3.3.6(7), respectivamente.

(4) Para secções com armaduras simétricas sujeitas a um esforço de compressão, é necessário considerar uma excentricidade mínima e_o = h/30 mas não inferior a 20 mm, em que h é a altura da secção.

5) Em partes de secções sujeitas a esforços aproximadamente centrados (e_d/h ≤ 0,1), como por exemplo os banzos comprimidos de vigas em caixão, a extensão média de compressão nessa parte da secção deverá ser limitada a ε_c2 (ou ε_c3 se se utilizar a relação bilinear da Figura 3.4).

(6) O domínio admissível de distribuições de extensões é o representado na Figura 6.1.

(7) Para elementos pré-esforçados com armaduras não aderentes de modo permanente, ver 5.10.8.

(8) Para armaduras de pré-esforço exteriores, considera-se que a extensão no aço de pré-esforço entre dois pontos de contacto sucessivos (ancoragens ou desviadores) é constante. A extensão no aço de pré-esforço é então igual à extensão inicial, obtida imediatamente após a conclusão da operação de pré-esforço, acrescida da extensão resultante da deformação da estrutura entre as zonas de contacto consideradas. Ver também 5.10.

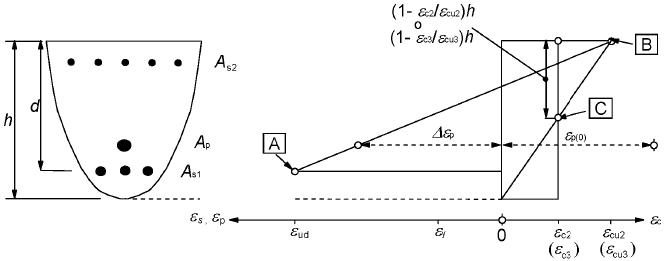
A - limite para a extensão de tracção do aço para betão armado
B - limite para a extensão de compressão do betão
C - limite para a extensão de compressão simples do betão

Figura 6.1 – Distribuições de extensões admissíveis no estado limite último

---

3.1 Betão
3.1.7 Relações tensões-extensões para o cálculo de secções transversais

(2) Poderão utilizar-se outras idealizações para a relação simplificada tensões-extensões na condição de serem equivalentes ou mais conservativas do que a definida em (1), por exemplo um diagrama bilinear como representado na Figura 3.4 (tensão e extensão de compressão, expressas em valor absoluto) com os valores de ε_c3 e ε_cu3 de acordo com o Quadro 3.1.

ε_c3(⁰/₀₀) = 1.75 para f_ck ≤ 50 MPa
ε_c3(⁰/₀₀) = 1,75 + 0,55[(f_ck - 50)/40] para 50 < f_ck ≤ 90 MPa

y

ε_cu3(⁰/₀₀) = 3.50 para f_ck ≤ 50 MPa
ε_cu3(⁰/₀₀) = 2.6 + 35[(90 - f_ck)/100]⁴ para 50 < f_ck ≤ 90 MPa

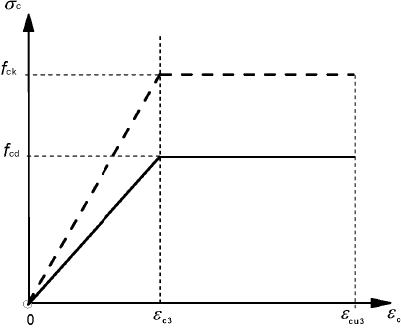
Figura 3.4 – Diagrama bilinear de tensões-extensões

(3) Poderá considerar-se uma distribuição rectangular de tensões (ver a Figura 3.5). O coeficiente λ, que define a altura útil da zona comprimida, e o coeficiente η, que define a resistência efectiva, são obtidos por:

y

NOTA: Se a largura da zona comprimida diminuir na direcção da fibra extrema mais comprimida, o valor η·f_cd deverá ser reduzido de 10%.

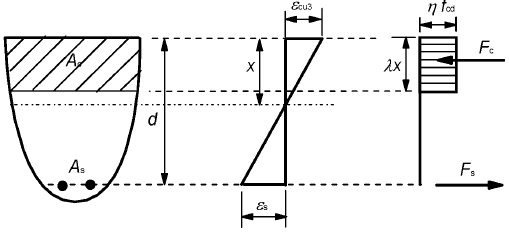
Figura 3.5 – Distribuição rectangular de tensões

3.2 Aço para betão armado
3.2.7 Hipóteses de cálculo

(2) Para o cálculo corrente, poderá admitir-se qualquer uma das seguintes hipóteses (ver a Figura 3.8):

• a) um ramo superior inclinado com uma extensão limite de ε_ud e uma tensão máxima de k·f_yk/γ_s, em que k= (f_t/f_y)_k;

NOTA 1: O valor de ε_ud a utilizar em Portugal é o seguinte:

• ε_ud = 0.90·ε_uk

NOTA 2: O valor de (f_t/f_y)_k é indicado no quadro C1 (Anexo C):

Quadro C.1 – Propriedades das armaduras

	Varões e fios
Classe	A	B	C
Valor característico da tensão de cedência fyk ou f0,2k (MPa)	400 à 600
Valor mínimo de k = (ft/fy)k	≥ 1,05	≥ 1,08	≥ 1,15
Valor característico da extensão à tensão máxima, εuk (%)	≥ 2,5	≥ 5,0	≥ 7,5

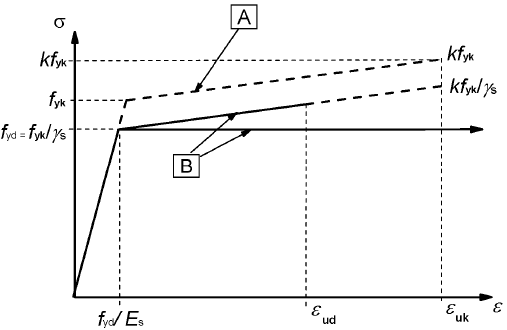
A- Diagrama idealizado; B- Diagrama de cálculo
Figura 3.8 – Diagramas tensões-extensões, idealizado e de cálculo, do aço das armaduras para betão armado (traccionado ou comprimido)

(3) O valor médio da massa volúmica poderá admitir-se igual a 7850 kg/m³.

(4) O valor de cálculo do módulo de elasticidade, Es, poderá admitir-se igual a 200 GPa.

---

Domínios de deformação

As deformações limite das seções, dependendo do tipo de solicitação, conduzem a admitir os seguintes domínios:

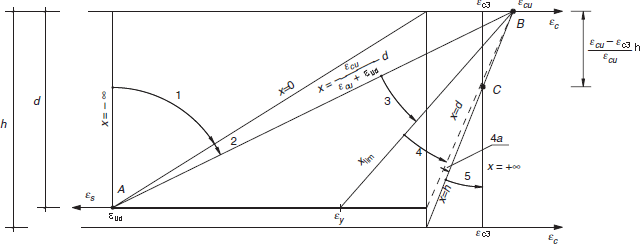
• Domínio 1: Tração simples ou composta em que toda a sessão está em tração. As linhas de deformação giram sobre o ponto A correspondente a uma extensão da armadura mais tracionada de ε_ud.
• Domínio 2: Flexão simples ou composta em que o betão não alcança a deformação de ruptura à flexão ε_cu3. As linhas de deformação giram sobre o ponto A.
• Domínio 3: Flexão simples ou composta em que as linhas de deformação giram sobre o ponto B correspondente à extensão de ruptura à flexão de betão ε_cu3 definida em 3.1.7. A extensão da armadura mais tracionada é compreendida entre ε_ud e ε_y, em que ε_y é a extensão correspondente à tensão de cedência do aço.
• Domínio 4: Flexão simples ou composta em que as linhas de deformação giram sobre o ponto B. A extensão da armadura mais tracionada é compreendida entre ε_y e 0.
• Domínio 4a: Flexão composta em que todas as armaduras estão comprimidas e existe uma pequena área de betão em tração. As linhas de deformação giram sobre o ponto B.
• Domínio 5: Compressão simples ou composta em que os dois materiais estão comprimidos. As linhas de deformação giram sobre o ponto C definido por a linha correspondente ao limite para a extensão de compressão simples do betão, ε_c3, definida em 3.1.7.

Chama-se eixo neutro da secção à linha de extensão zero. A distância a partir da fibra mais comprimida é representada pelo símbolo "x".

A variação do eixo neutro de - ∞ até + ∞ , determina todas as combinações possíveis de momento de flexão e força axial últimos na seção.

Verificação das secções rectangulares

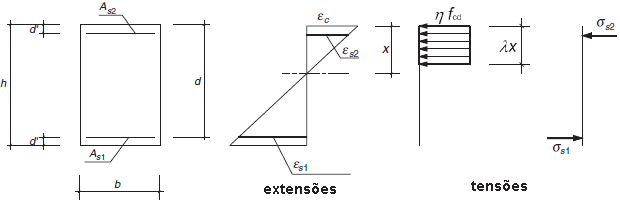
As equações de equilíbrio que determinam o momento e força axial resistentes (Mu e Nu) são as seguintes:
(diagrama de interação axial-momento)

Domínio 1:

- ∞ < x ≤ 0

• N_u(x) = - A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u (x)= - A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(d'-x)/(d-x)

Domínio 2:

0 < x ≤ d · ε_cu/(ε_cu+ε_ud)

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u(x)= η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(x-d')/(d-x)

Domínio 3:

d · ε_cu/(ε_cu+ε_ud) < x ≤ x_lim

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Domínio 4:

x_lim< x ≤ d

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Domínio 4a:

d < x ≤ h

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u/x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(x-d)/x

Domínio 5:

h < x < ∞

• N_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b·[h/2-[1- (1-λ)·h/x]·h/2] + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_c3·(x-d')/(x-h/2)
• ε_s1(x) = ε_c3·(x-d)/(x-h/2)