7.2 Limitación de tensiones

(1)P La tensión de compresión en el hormigón se debe limitar con el fin de evitar fisuras longitudinales, micro fisuras o altos niveles de fluencia, que podrían producir efectos inaceptables en la función de la estructura.

(2) Las fisuras longitudinales se pueden producir si el nivel de tensiones, bajo la combinación característica de cargas, supera un valor crítico. Tal fisuración puede producir una reducción de la durabilidad. En ausencia de otras medidas, tales como un aumento en el recubrimiento de la armadura en la zona comprimida o un confinamiento mediante armadura transversal, puede ser apropiado limitar la tensión de compresión a un valor k₁·f_ck en áreas expuestas a ambientes de clases de exposición XD,XF y XS (véase la tabla 4.1).

NOTA El valor de k₁ para uso en España es el siguiente:

• k₁ = 0.6

(4)P Se deben limitar las tensiones de tracción en la armadura con el fin de evitar una deformación unitaria anelástica, una fisuración o una deformación inaceptables.

(5) Se puede suponer que si la tensión de tracción en la armadura no supera k₃f_yk, bajo la combinación característica de acciones, se evita una fisuración o una deformación de apariencia inaceptable. Donde la tensión de tracción se produzca por una deformación impuesta, la tensión de tracción no debería superar k₄f_yk.El valor medio de la tensión en tendones de pretensado no debería supera k₅f_yk.

NOTA Los valores de k₃, k₄ y k₅ para uso en España son los siguientes:

• k₃ = 0.80
• k₄ = 1.00
• k₅ = 0.75

7.3 Control de fisuras

7.3.1 Consideraciones generales

(1)P La fisuración se debe limitar a una región que no afecte al correcto funcionamiento o la durabilidad de la estructura, o produzca una apariencia inaceptable.

(2) La fisuración es normal en estructuras de hormigón armado sometidas a flexión, cortante, torsión o tracción, producidos por carga directa, coacciones o deformaciones impuestas.

(3) Las fisuras también se pueden producir por otras causas tales como retracción plástica o reacciones químicas expansivas dentro del hormigón endurecido. Tales fisuras pueden ser inaceptablemente grandes pero su prevención y control queda fuera del alcance de este apartado.

(4) Se puede permitir la formación de fisuras sin ningún intento por controlar su abertura, siempre y cuando no perjudiquen al funcionamiento de la estructura.

(5) Se debería establecer un valor límite, w_max, para la abertura de fisura calculada, w_k, teniendo en cuenta la función prevista y la naturaleza de la estructura y los costes de limitar la fisuración.

NOTA Los valores de w_max para uso en España son los siguientes:

Tabla AN/9 (Tabla 7.1N).Abertura máxima de la fisura

Clase de exposición	wmax (mm)
	Hormigón armado (para la combinación cuasipermanente de acciones)	Hormigón pretensado (para la combinación frecuente de acciones)
XO(2), XC1(4)	0.4	0.2
XC1(4), XC2, XC3, XF1, XF3, XC4	0.3	0.2(1)
XS1, XS2, XD1, XD2, XD3, XF2, XF4, XA1(3)	0.2	Descompresión
XS3, XA2(3), XA3(3)	0.1
(1) Adicionalmente deberá comprobarse que las armaduras activas se encuentran en la zona comprimida de la sección, bajo la combinación cuasipermanente de acciones. (2) Para las clases de exposición XO y XC1, la abertura de fisura no influye normalmente en la durabilidad. Los valores recogidos en la tabla para estos casos se establecen para garantizar un aspecto aceptable. (3) La limitación relativa a las clases XA1, XA2 y XA3 sólo será de aplicación en el caso de que el ataque químico pueda afectar a la armadura. En otros casos, se aplicará la limitación correspondiente a la clase general correspondiente. (4) La definición de la clase XC1 recogida en el Eurocódigo se corresponde parcialmente con las clases I y IIa definidas en la Instrucción de Hormigón Estructural EHE-08, por lo que el Autor del proyecto aplicará la limitación menos exigente de la apertura de fisura recogida en la segunda fila de la tabla, sólo cuando se trate de elementos interiores de edificios protegidos de la intemperie.

(6) Para elementos que cuenten sólo con armaduras activas no adherentes, se aplican los requisitos para elementos de hormigón armado. Para elementos que cuenten con una combinación de armadura activas adherente y no adherentes, se aplican los requisitos para elementos de hormigón pretensado con armadura activa adherente.

(7) Puede ser necesario tomar medidas especiales para elementos sujetos a una clase de exposición XD3. La elección de medidas apropiadas dependerá de la naturaleza del agente agresivo involucrado.

(8) Cuando se usan modelos de bielas y tirantes con las bielas orientadas de acuerdo con las trayectorias de las tensiones de compresión en el estado no fisurado, es posible usar las fuerzas en los tirantes para obtener las correspondientes tensiones en el acero para estimar la abertura de fisura [véase el punto (2) del apartado 5.6.4].

(9) La abertura de fisura se puede calcular de acuerdo con el apartado 7.3.4. Una alternativa simplificada es limitar el diámetro de la barra o la separación entre ellas, conforme al apartado 7.3.3.

7.3.4 Cálculo de las aberturas de fisura

(1) La abertura de fisura, w_k, se puede calcular a partir de la ecuación (7.8):

donde

• s_r,max es la separación máxima entre fisuras;
• ε_sm es el alargamiento unitaria medio en la armadura bajo la combinación relevante de cargas, incluido el efecto de deformaciones impuestas y teniendo en cuenta los efectos de la rigidización por la colaboración del hormigón entre fisuras. Sólo se considera el alargamiento por tracción adicional más allá del estado de deformación cero del hormigón al mismo nivel;
• ε_cm es la deformación unitaria media en el hormigón entre fisuras.

(2) Se puede calcular ε_sm - ε_cm a partir de la ecuación:

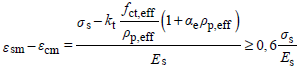
donde:

• σ_s es la tensión en la armadura de tracción considerando la sección fisurada. Para elementos con armadura pretesa, σ_s se puede reemplazar por Δσ_p la variación de tensiones en las armaduras activas a partir del estado de tensión cero del hormigón al mismo nivel;
• α_e es la relación E_s/E_em
• ρ_p,eff = (A_s + ξ₁ A'_p)/A_c,eff
  (7.10)
  
  A'_p y A_c,eff como se definen en el punto (3) del apartado 7.3.2;
  A_c,eff es el área eficaz del hormigón en tracción que rodea la armadura pasiva o la activa, de canto h_c,ef, donde h_c,ef es el menor valor entre 2.5(h-d), (h-x)/3 o h/2 (véase la figura 7.1);.

  a) Viga
  
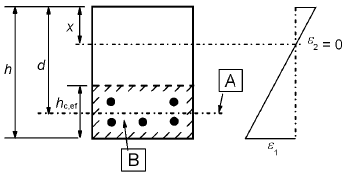
   A   nivel del centro de gravedad de la armadura     B   área eficaz de tracción, A_c,eff

  b) Losa
  
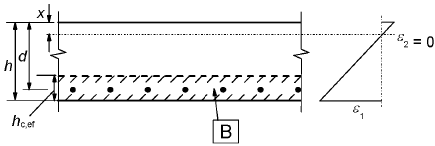
   B   área eficaz de tracción, A_c,eff

  c) Elemento en tracción
  
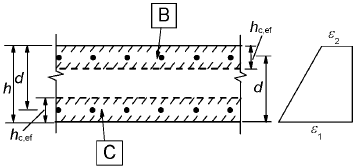
   B   área eficaz de tracción para la cara superior, A_ct,eff
   C   área eficaz de tracción para la cara inferior, A_cb,eff

  Figura 7.1 - Área eficaz de tracción (casos típicos)

• ξ₁ conforme a la ecuación (7.5);
• k_t es un coeficiente dependiente de la duración de la carga.
  k_t = 0,6 para carga a corto plazo
  k_t = 0,4 para carga a largo plazo

(3) En situaciones donde la armadura adherente se dispone con unos centros razonablemente cercanos dentro de la zona de tracción (distancia ≤ 5(c+Φ/2)), se puede calcular la distancia máxima final entre fisuras a partir de la ecuación (7.11) (véase la figura 7.2):

donde:

• Φ es el diámetro de la barra. Cuando en una sección se utilizan varios diámetros, se debería usar un diámetro equivalente, Φ_eq. Para una sección con n₁ barras de Φ₁ de diámetro y barras n₂ de diámetro Φ₂, se debería usar la siguiente ecuación:
  
• Φ_eq = (n₁·Φ₁² + n₂·Φ₂²) / (n₁·Φ₁ + n₂·Φ₂)
  (7.12)
  
  
• c: es el recubrimiento de la armadura longitudinal;
• k₁: es un coeficiente que considera las propiedades de adherencia de la armadura adherente:
  = 0,8 para barras de alta adherencia
  = 1,6 para barras con una superficie lisa (por ejemplo, armaduras activas)
• k₂ es un coeficiente que considera la distribución de las deformaciones unitarias:
  = 0,5 para flexión
  = 1,0 para tensión pura.
  En el caso de tensión excéntrica o para áreas locales, se deberían usar valores intermedios de k₂ que se pueden calcular a partir de la ecuación:
  
  k₂ = (ε₁ + ε₂) / (2·ε₁)
  (7.13)
  
  donde ε₁ es la mayor y ε₂ es la menor deformación unitaria a tracción en las fibras extremas de la sección considerada, suponiendo la sección fisurada.

NOTA Los valores de k₃ y k₄ para uso en España son los siguientes:

• k₃ = 3.4
• k₄ = 0.425

Si las distancias entre las barras de la armadura adherente supera 5(c+Φ/2) (véase la figura 7.2) o si no hay armadura adherente dentro de la zona de tracción, se puede obtener un límite superior de la abertura de fisuras suponiendo una separación entre fisuras máxima de:

(5) Para muros sometidos a retracciones térmicas tempranas, en las que la zona de acero horizontal, As no cumple con los requisitos del apartado 7.3.2 y en las que la parte inferior del muro está coaccionada por una base hormigonada previamente, se puede suponer s_r,max igual a 1,3 veces la altura del muro..

---

Cálculo de secciones en servicio con fisuración

Hipótesis básicas.

Las hipótesis adoptadas, para la determinación de las expresiones que se presentan, son las siguientes:

• El plano de deformaciones se mantiene plano después de la deformación.
• Adherencia perfecta entre el hormigón y el acero.
• Comportamiento lineal para el hormigón comprimido.
• Se desprecia la resistencia a tracción del hormigón.
• Comportamiento lineal para los aceros, tanto en tracción como en compresión.

Sección rectangular

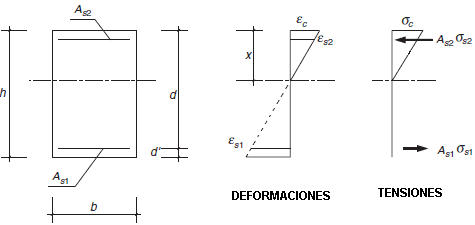
Las ecuaciones que definen el comportamiento de la sección son:
(compresión: signo positivo; tracción: signo negativo)

• N_k = 1/2·b·x·σ_c + A_s2·σ_s2 + A_s1·σ_s1
• M_k = 1/2·b·x·σ_c·(h/2-x/3) + A_s2·σ_s2·(h/2-d') + A_s1·σ_s1·(h/2-d)
• σ_s1 = E_s·ε_s1 = Es·ε_c·(x-d)/x; |σ_s1| ≤ k₃·f_yk
• σ_s2 = E_s·ε_s2 = Es·ε_c·(x-d')/x
• σ_c = E_cm·ε_c≤ k₁· f_ck

En elementos sometidos a flexión simple (N_k=0)

• Profundidad relativa de la fibra neutra:
  
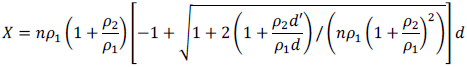
• Inercia fisurada:
  I_cr = nA_s1(d-X)(d-X/3) + nA_s2(X-d')(X/3-d')


• Tensión de compresión en la fibra más comprimida de hormigón:
  σ_c = M_k · X / I_cr
  
  donde n= E_s/E_cm; ρ₁ = A_s1/(bd); ρ₂ = A_s2/(bd)