Estado límite de fisuración
RESULTADO
Máxima tensión de compresión en el hormigón
| Tensión de compresión | Tensión de compresión límite | Condición |
| σc (MPa) | σc,max (MPa) | σc < σc,max |
| 8.41 | 15 | CUMPLE |
Máxima tensión de tracción en la armadura
| Tensión de tracción | Tensión de tracción límite | Condición |
| σs1 (MPa) | σs1,max (MPa) | σs1 < σs1,max |
| 175.74 | 400 | CUMPLE |
Abertura de fisura
| Separación entre fisuras | Deformación media | Abertura de fisura |
| sr,max (cm) | εsm - εcm (‰) | Wk (mm) |
| 26.3 | 0.53 | 0.14 |
DETALLES DEL CÁLCULO
Notación y metodología según Art 7 de EC2
Cálculo de tensiones suponiendo la sección fisurada
- Tensión de tracción en la armadura
σs1 = n·σc·(d-X)/X = 6.35·8.41·(25.7-5.99)/5.99 = 175.74 MPa - Máxima tensión de tracción en la armadura
σs1,max = k3 · fyk = 0.8 · 500 = 400 MPa - Tensión de compresión en la fibra más comprimida de hormigón
σc = Mk · X / Icr = 8.41 MPa - Máxima tensión de compresión en el hormigón
σc,max = k1 · fck = 0.6 · 25 = 15 MPa
donde
- n= Es / Ecm = 200 / 31.48 = 6.35
Ecm = 22·[fcm/10]0.3 = 22·[33/10]0.3 = 31.48 GPa
fcm = fck + 8 = 25 + 8 = 33 MPa - d (canto útil) = h – c - Φ/2 = 30 – 3.5 – 1.6/2 = 25.7 cm
- X (Profundidad de la fibra neutra) = 5.99 cm
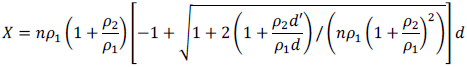
con:- d′ = h - d = 30 - 25.7 = 4.3 cm
- ρ1 = As1 / (b·d) = 6.03 / (40·25.7) = 0.0059
- ρ2 = As2 / (b·d) = 3.39 / (40·25.7) = 0.0033
- Icr (inercia de sección fisurada) = 17811.96 cm4
Icr = n·As1·(d-X)·(d-X/3) + n·As2·(X-d′)·(X/3-d′)
Icr = 6.35·6.03·(25.7-5.99)·(25.7-5.99/3) + 6.35·3.39·(5.99-4.3)·(5.99/3-4.3) = 17811.96 cm4
Cálculo de la abertura de fisura
wk = sr,msx·(εsm - εcm) = 263.4 · 0.00053 = 0.14 mm
donde
εsm - εcm (diferencia entre deformaciones medias) = 0.00053
εsm - εcm = max(εm,1 ; εm,2) = max(0.00042 ; 0.00053)
con:
- εm,1 = [σs1 - kt·(fct,eff/ρp,eff)·(1+αe·ρp,eff)] / Es
εm,1 = [175.74 - 0.6·(2.56/0.0188)·(1+6.35·0.0188)] / 200000 = 0.00042
- kt = 0.6 (Larga duración)
- fct,eff = fctm = 2.56 MPa
fctm = 0,30 × fck(2/3) = 0,30 × 25(2/3) = 2.56 MPa - ρp,eff = As / Ac,eff = 6.03 / 320.08 = 0.0188
Ac,eff = b · hc,ef = 40 · 8 = 320.08 cm2
hc,ef = min[2.5(h-d) ; (h-X)/3 ; h/2] = min[10.75 ; 8 ; 15] cm - αe = Es / Ecm = 6.35
- εm,2 = 0.6 · σs / Es = 0.6 · 175.74 / 200000 = 0.00053
sr,msx (separación máxima entre fisuras) = 26.34 cm
(caso sep.barras = 170 mm ≤ 5(c+Φ/2) = 215 mm)
sr,msx = k3·c + k1·k2·k4·Φ/ρp,eff
sr,msx = 3.4·35 + 0.8·0.5·0.425·16/0.0188 = 263.38 mm
con:
- k1 = 0.8 (barras de alta adherencia)
- k2 = 0.5 (flexión)





