EHE08: Estado límite Momento flector - Axil
Artículo 42. Estado Límite de Agotamiento frente a solicitaciones normales
42.1.2 Hipótesis básicas
El cálculo de la capacidad resistente última de las secciones se efectuará a partir de las hipótesis generales siguientes:
a) El agotamiento se caracteriza por el valor de la deformación en determinadas fibras de la sección, definidas por los dominios de deformación de agotamiento detallados en 42.1.3.
b) Las deformaciones del hormigón siguen una ley plana. Esta hipótesis es válida para piezas en las que la relación entre la distancia entre puntos de momento nulo y el canto total, es superior a 2.
c) Las deformaciones εs de las armaduras pasivas se mantienen iguales a las del hormigón que las envuelve.
d) El diagrama de cálculo tensión-deformación del hormigón es alguno de los que se definen en 39.5. No se considerará la resistencia del hormigón a tracción.
El diagrama de cálculo tensión-deformación del acero de las armaduras pasivas es el que se define en 38.4.
e) Se aplicarán a las resultantes de tensiones en la sección las ecuaciones generales de equilibrio de fuerzas y momentos. De esta forma podrá calcularse la capacidad resistente última mediante la integración de las tensiones en el hormigón y en las armaduras activas y pasivas.
39.5 Diagrama de cálculo tensión-deformación del hormigón
Para hormigones con fck ≤ 50 N/mm2, se consideran los siguientes valores:
- Deformación de rotura a compresión simple, εc0 = 0.002
- Deformación última en flexión, εcu = 0.0035
b) Diagrama rectangular
Está formado por un rectángulo cuya profundidad λ(x) · h, e intensidad η(x) · fcd dependen de la profundidad del eje neutro x (figura 39.5.b), y de la resistencia del hormigón. Sus valores para hormigones con fck ≤ 50 N/mm2, son:
- η(x) = 1
- λ(x) = 0.8·x/h, si 0 < x ≤ h
- λ(x) = 1- 0.2·h/x, si h < x < ∞
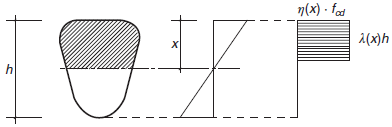
Figura 39.5.b. Diagrama de cálculo rectángular
38.4 Diagrama de cálculo tensión-deformación del acero en armaduras pasivas
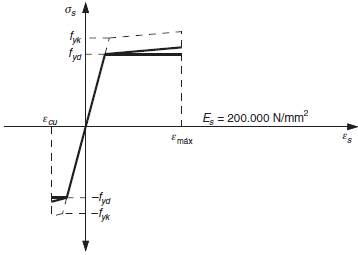
Figura 38.4. Diagrama tensión-deformación de cálculo en las armaduras pasivas
Se adoptará una deformación máxima del acero en tracción en el cálculo εmáx = 0,01.
En general, es suficiente la utilización del diagrama de cálculo bilineal con rama horizontal a partir del límite elástico y tomando como módulo de deformación longitudinal del acero Es = 200.000 N/mm2.
42.1.3 Dominios de deformación
Las deformaciones límite de las secciones, según la naturaleza de la solicitación, conducen a admitir los siguientes dominios (figura 42.1.3):
Dominio 1: Tracción simple o compuesta en donde toda la sección está en tracción. Las rectas de deformación giran alrededor del punto A correspondiente a un alargamiento de la armadura más traccionada del 10 por 1.000.
Dominio 2: Flexión simple o compuesta en donde el hormigón no alcanza la deformación de rotura por flexión. Las rectas de deformación giran alrededor del punto A.
Dominio 3: Flexión simple o compuesta en donde las rectas de deformación giran alrededor del punto B correspondiente a la deformación de rotura por flexión del hormigón εcu definida en el apartado 39.5. El alargamiento de la armadura más traccionada está comprendido entre 10 por 1.000 y εy, siendo εy, el alargamiento correspondiente al límite elástico del acero.
Dominio 4: Flexión simple o compuesta en donde las rectas de deformación giran alrededor del punto B. El alargamiento de la armadura más traccionada está comprendido entre εy y 0.
Dominio 4a: Flexión compuesta en donde todas las armaduras están comprimidas y existe una pequeña zona de hormigón en tracción. Las rectas de deformación giran alrededor del punto B.
Dominio 5: Compresión simple o compuesta en donde ambos materiales trabajan a compresión. Las rectas de deformación giran alrededor del punto C definido por la recta correspondiente a la deformación de rotura del hormigón por compresión, εc0 definido en el apartado 39.5.
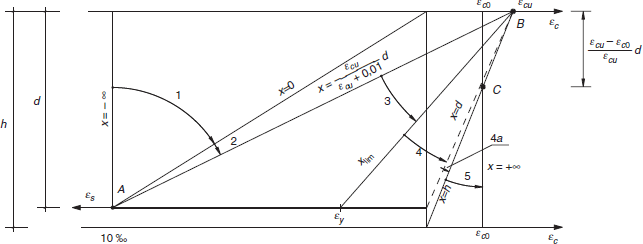
Figura 42.1.3.
Se denomina eje neutro de una sección a la recta de deformación nula. Su distancia a la fibra más comprimida se designa por x.
El acortamiento máximo del hormigón se fija en εcu en flexión y en εc0 en compresión simple.
42.1.4 Comprobación de secciones.
A partir de las hipótesis básicas definidas en 42.1.2, es posible plantear las ecuaciones de equilibrio de la sección, que constituyen un sistema de ecuaciones no lineales.
En el caso de comprobación, se conocen la forma y dimensiones de la sección de hormigón, la posición y cuantía de la armadura y las características de los materiales y son incógnitas el plano de deformación de agotamiento (x) y los esfuerzos resistentes de la sección (Nu y Mu).
Aplicación al caso de secciones rectangulares
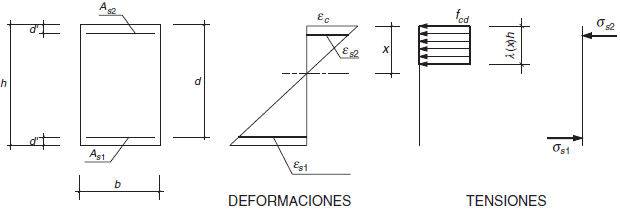
Las ecuaciones de equilibrio que determinan los puntos de solicitaciones normales últimas (diagrama de interacción momento-axil) son las siguientes
Dominio 1:
- ∞ < x ≤ 0
- Nu(x) = - As2·σs2(x) - As1·fyd
- Mu (x)= - As2·σs2(x)·(h/2-d') - As1·fyd·(h/2-d)
- σs2(x) = Es · εs2(x) = Es·0.01·(d'-x)/(d-x) ≤ fyd
Dominio 2:
0 < x ≤ d · εcu/(εcu+0.01)
- Nu(x) = 1·fcd·0.8·x·b + As2·σs2(x) - As1·fyd
- Mu(x)= 1·fcd·0.8·x·b·(h/2-0.8·x/2) + As2·σs2(x)·(h/2-d') - As1·fyd·(h/2-d)
- σs2(x) = Es · εs2(x) = Es·0.01·(x-d')/(d-x) ≤ fyc,d
Dominio 3:
d · εcu/(εcu+0.01) < x ≤ xlim
- Nu(x) = 1·fcd·0.8·x·b + As2·σs2(x) - As1·fyd
- Mu(x) = 1·fcd·0.8·x·b·(h/2-0.8·x/2) + As2·σs2(x)·(h/2-d') - As1·fyd·(h/2-d)
- σs2(x) = Es · εs2(x) = Es·0.0035·(x-d')/x ≤ fyc,d
Dominio 4:
xlim< x ≤ d
- Nu(x) = 1·fcd·0.8·x·b + As2·fyc,d - As1·σs1(x)
- Mu(x) = 1·fcd·0.8·x·b·(h/2-0.8·x/2) + As2·fyc,d·(h/2-d') - As1·σs1(x)·(h/2-d)
- σs1(x) = Es · εs1(x) = Es·0.0035·(d-x)/x ≤ fyd
Dominio 4a:
d < x ≤ h
- Nu(x) = 1·fcd·0.8·x·b + As2·fyc,d + As1·σs1(x)
- Mu/x) = 1·fcd·0.8·x·b·(h/2-0.8·x/2) + As2·fyc,d·(h/2-d') + As1·σs1(x)·(h/2-d)
- σs1(x) = Es · εs1(x) = Es·0.0035·(x-d)/x ≤ fyc,d
Dominio 5:
h < x < ∞
- Nu(x) = 1·fcd·(1- 0.2·h/x)·h·b + As2·fyc,d + As1·σs1(x)
- Mu(x) = 1·fcd·(1- 0.2·h/x)·h·b·[h/2-(1- 0.2·h/x)·h/2] + As2·fyc,d·(h/2-d') + As1·σs1(x)·(h/2-d)
- σs1(x) = Es · εs1(x) = Es·0.002·(x-d)/(x-3·h/7) ≤ fyc,d




