Artículo 43º Estado Límite de Inestabilidad

43.1 Generalidades

43.1.1 Definiciones

A los efectos de aplicación de este Artículo 43° se denominan:

• Estructuras intraslacionales aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.
• Estructuras traslacionales aquellas cuyos nudos, bajo solicitaciones de cálculo, presentan desplazamientos transversales cuyos efectos no pueden ser despreciados desde el punto de vista de la estabilidad del conjunto.
• Soportes aislados, los soportes isostáticos, o los de pórticos en los que puede suponerse que la posición de los puntos donde se anula el momento de segundo orden no varía con el valor de la carga.
• Esbeltez mecánica de un soporte de sección constante, el cociente entre la longitud de pandeo l₀ del soporte (distancia entre puntos de inflexión de la deformada) y el radio de giro i de la sección bruta de hormigón en la dirección considerada.
• Esbeltez geométrica de un soporte de sección constante, el cociente entre la longitud de pandeo l₀ del soporte y la dimensión (b ó h) de la sección que es paralela al plano de pandeo.

COMENTARIOS

La comprobación a pandeo de la estructura en su globalidad o de los soportes aisladamente deberá hacerse atendiendo a la traslacionalidad o intraslacionalidad de la misma, y a los criterios establecidos en 43.3 y 43.4.

En pórticos planos, las longitudes de pandeo l₀ en el plano considerado, pueden obtenerse de

l₀ = α · L

donde

• L: longitud real del elemento
• α: Factor de longitud de pandeo

Para pórticos intraslacionales:

Para pórticos traslacionales:

• Ψ: Relación de rigideces Σ[EI/L] de los soportes a Σ[EI/L] de las vigas, en cada extremo A y B del soporte considerado. Como valor de I se tomará la inercia bruta de la sección.
  (Extremo empotrado Ψ = 0; Extremo articulado Ψ = ∞ )

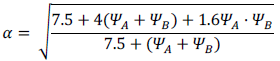
Algunos casos particulares son:

• Pórticos intraslacionales:
  1 Soporte biempotrado (α = 0,5)
  2 Soporte biarticulado (α = 1,0)
  3 Soporte articulado-empotrado (α = 0,7)
• Pórticos traslacionales:
  4 Soporte en ménsula (α = 2,0)
  5 Soporte biempotrado con extremos desplazables (α = 1,0)

43.1.2 Campo de aplicación

Este artículo concierne a la comprobación de soportes aislados, estructuras aporticadas y estructuras reticulares en general, en los que los efectos de segundo orden no pueden ser despreciados.

La aplicación de este artículo está limitada a los casos en que pueden despreciarse los efectos de torsión.

Esta Instrucción no cubre los casos en que la esbeltez mecánica de los soportes es superior a 200.

En soportes aislados, los efectos de segundo orden pueden despreciarse si la esbeltez mecánica es inferior a una esbeltez límite asociada a una perdida de capacidad portante del soporte del 10% respecto de un soporte no esbelto. La esbeltez límite inferior λ_inf puede aproximarse por la siguiente expresión:

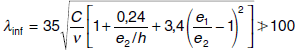
donde:

• ν: Axil adimensional o reducido de cálculo que solicita el soporte.
  
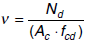
• e₂: Excentricidad de primer orden en el extremo del soporte con mayor momento, considerada positiva.
• e₁: Excentricidad de primer orden en el extremo del soporte con menor momento, positiva si tiene el mismo signo que e₂.
  En estructuras traslacionales se tomará e1/e2 igual a 1,0.
• h: Canto de la sección en el plano de flexión considerado.
• C: Coeficiente que depende de la disposición de armaduras cuyos valores son:
  0,24 para armadura simétrica en dos caras opuestas en el plano de flexión.
  0,20 para armadura igual en las cuatro caras.
  0,16 para armadura simétrica en las caras laterales.

43.3 Comprobación de estructuras intraslacionales

En las estructuras intraslacionales, el cálculo global de esfuerzos podrá hacerse según la teoría de primer orden. A partir de los esfuerzos así obtenidos, se efectuará una comprobación de los efectos de segundo orden de cada soporte considerado aisladamente, de acuerdo con 43.5, y con la longitud de pandeo de acuerdo con lo indicado en 43.1.1-comentarios.

43.4 Comprobación de estructuras traslacionales

Las estructuras traslacionales serán objeto de una comprobación de estabilidad de acuerdo con las bases generales de 43.2.

Para las estructuras usuales de edificación de menos de 15 plantas, en las que el desplazamiento máximo en cabeza bajo cargas horizontales características, calculado mediante la teoría de primer orden y con las rigideces correspondientes a las secciones brutas, no supere 1/750 de la altura total, basta comprobar cada soporte aisladamente con los esfuerzos obtenidos aplicando la teoría de primer orden y con la longitud de pandeo de acuerdo con lo indicado en 43.1.1-comentarios.

43.5 Comprobación de soportes aislados

Para soportes con esbeltez mecánica comprendida entre λ_inf y 100 puede aplicarse el método aproximado de 43.5.1 ó 43.5.2.

Para soportes con esbeltez mecánica comprendida entre 100 y 200 se aplicará el método general establecido en 43.2.

43.5.1 Método aproximado. Flexión compuesta recta

Para soportes de sección y armadura constante deberá dimensionarse la sección para una excentricidad total igual a la que se indica:

e_tot = e_e + e_a ≥ e₂

donde:

• e_a: Excentricidad ficticia utilizada para representar los efectos de segundo orden
  
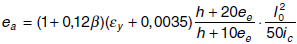
• e_e: Excentricidad de cálculo de primer orden equivalente.
  e_e = 0.6·e₂ + 0.4·e₁ ≥ 0.4·e₂ para soportes intraslacionales;
  e_e = e₂ para soportes traslacionales
• e₁, e₂: Excentricidades del axil en los extremos de la pieza definidas en 43.1.2.
• l₀: Longitud de pandeo.
• i_c: Radio de giro de la sección de hormigón en la dirección considerada.
• h: Canto total de la sección de hormigón.
• e_y: Deformación del acero para la tensión de cálculo f_yd, es decir,
  e_y = f_yd / E_s
• β: Factor de armado, dado por
  en secciones rectangulares
  
  • β = 1.0, para armadura simétrica en dos caras opuestas en el plano de flexión.
  • β = 1.5, para armadura igual en las cuatro caras.
  • β = 3.0, para armadura simétrica en las caras laterales.
  en secciones circulares
  
  • β = 2.0