6.1 Bending with or without axial force

(1)P This section applies to undisturbed regions of beanls, slabs and similar types of members for which sections remain approximately plane before and after loading. The discontinuity regions of beams and other members in which plane sections do not remain plane may be designed and detailed according to 6.5.

(2)P When determining the ultinlate moment resistance of reinforced or prestressed concrete cross-sections, the following assumptions are made:

• plane sections remain plane.
• the strain in bonded reinforcement or bonded prestressing tendons, whether in tension or in compression, is the same as that in the surrounding concrete.
• the tensile strength of the concrete is ignored.
• the stresses in the concrete in compression are derived from the design stress/strain relationship given in 3.1.7.
• the stresses in the reinforcing or prestressing steel are derived from the design curves in 3.2 (Figure 3.8) and 3.3 (Figure 3.10).
• the initial strain in prestressing tendons is taken into account when assessing the stresses in the tendons.

(3)P The compressive strain in the concrete shall be limited to ε_cu2, or ε_cu3, depending on the stress-strain diagram used, see 3.1.7 and Table 3.1. The strains in the reinforcing steel and the prestressing steel shall be limited to ε_ud (where applicable); see 3.2.7 (2) and 3.3.6 (7) respectively.

(4) For cross-sections loaded by the compression force it is necessary to assume the minimum eccentricity, e_o = h/30 but not less than 20 mm where h is the depth of the section.

5) In parts of cross-sections which are subjected to approximately concentric loading (e_d/h ≤ 0,1), such as compression flanges of box girders, the mean compressive strain in that part of the section should be limited to ε_c2 (or ε_c3 if the bilinear relation of Figure 3.4 is used)

(6) The possible range of strain distributions is shown in Figure 6.1.

(7) For prestressed members with permanently unbonded tendons see 5.10.8.

(8) For external prestressing tendons the strain in the prestressing steel between two subsequent contact points (anchors or deviation saddles) is assumed to be constant. The strain in the prestressing steel is then equal to the initial strain, realised just after completion of the prestressing operation, increased by the strain resulting from the structural deformation between the contact areas considered. See also 5.10.

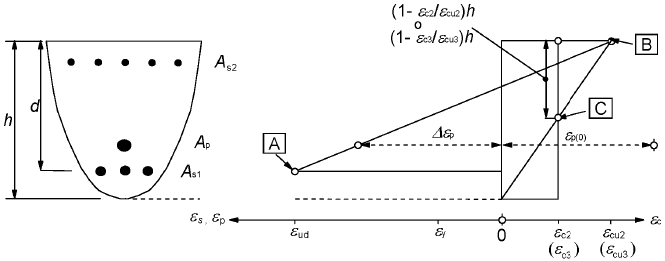
A- reinforcing steel tension strain limit
B - concrete compression strain limit
C - concrete pure compression strain limit

Figure 6.1: Possible strain distributions in the ultimate limit state

---

3.1 Concrete
3.1.7 Stress-strain relations for the design of cross-sections

(2) Other simplified stress-strain relationships may be used if equivalent to or more conservative than the one defined in (1), for instance bi-linear according to Figure 3.4 (compressive stress and shortening strain shown as absolute values) with values of ε_c3 and ε_cu3 according to Table 3.1.

ε_c3(⁰/₀₀) = 1.75 for f_ck ≤ 50 MPa
ε_c3(⁰/₀₀) = 1,75 + 0,55[(f_ck - 50)/40] for 50 < f_ck ≤ 90 MPa

and

ε_cu3(⁰/₀₀) = 3.50 for f_ck ≤ 50 MPa
ε_cu3(⁰/₀₀) = 2.6 + 35[(90 - f_ck)/100]⁴ for 50 < f_ck ≤ 90 MPa

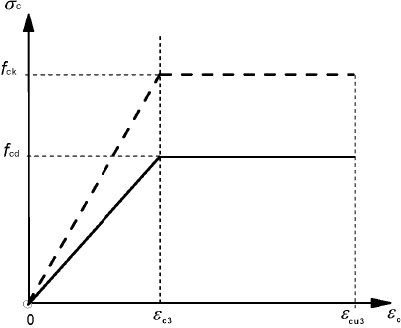
Figure 3.4: Bi-linear stress-strain relation.

(3) A rectangular stress distribution (as given in Figure 3.5) may be assumed. The factor λ, defining the effective height of the compression zone and the factor η, defining the effective strength, follow from:

and

Note: If the width of the compression zone decreases in the direction of the extreme compression fibre, the value η·f_cd should be reduced by 10%.

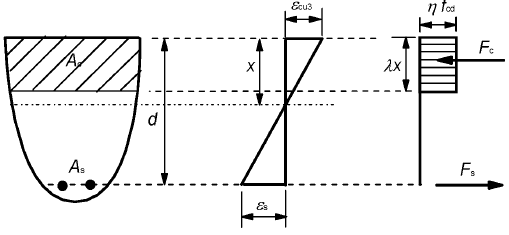
Figure 3.5: Rectangular stress distribution

3.2 Reinforcing steel
3.2.7 Design assumptions

(2) For normal design, the following assumptions may be made (see Figure 3.8):

• a) an inclined top branch with a strain limit of ε_ud and a maximum stress of k·f_yk/γ_s, where k= (f_t/f_y)_k;

Note 1: The value of ε_ud for use in a Country may be found in its National Annex. The recommended value is 0.90·ε_uk

Note 2: The value of (f_t/f_y)_k is given in Annex C (table C1).

Table C.1: Properties of reinforcement

	Bars and de-coiled rods
Class	A	B	C
Characteristic yield strength fyk or f0,2k (MPa)	400 a 600
Minimum value of k = (ft/fy)k	≥ 1,05	≥ 1,08	≥ 1,15
Characteristic strain at maximum force, εuk (%)	≥ 2,5	≥ 5,0	≥ 7,5

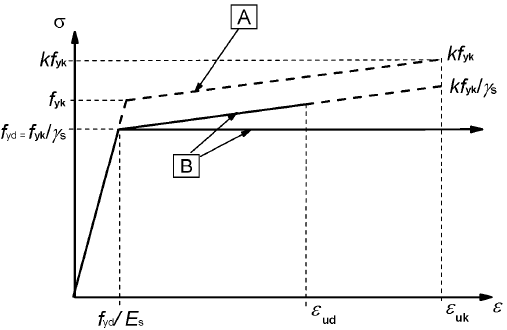
A- Idealised; B- Design
Figure 3.8: Idealised and design stress-strain diagrams for reinforcing steel (for tension and compression)

(3) The mean value of density may be assumed to be 7850 kg/m³.

(4) The design value of the modulus of elasticity, Es may be assumed to be 200 GPa.

---

Strain envelopes

The limit stains in sections, depending on the type of stress, enable the following ranges to be recognised:

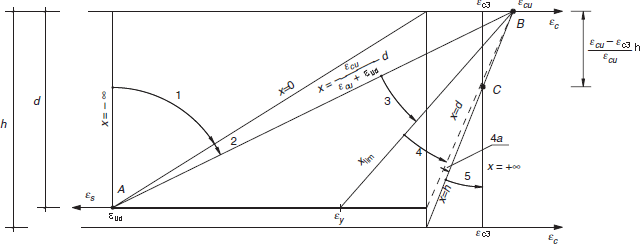
• Range 1: Pure or combined tension where the entire section is under tension. The strain lines turn about point A corresponding to an elongation in the reinforcement of the most tensioned of ε_ud.
• Range 2: Pure or combined bending, in which the concrete does not reach the ultimate bending strain. The strain lines turn about point A.
• Range 3: Pure or combined bending, in which the strain lines turn about point B corresponding to the ultimate bending strain of the concrete ε_cu3 defined in paragraph 3.1.7. The elongation of the most tensioned reinforcement is between ε_ud and ε_y (the elongation corresponding to the yield stress of the steel).
• Range 4: Single or combined bending in which the strain lines turn around point B. The elongation of the most tensioned reinforcement is between ε_y and 0.
• Range 4a: Combined bending in which all the reinforcements are compressed and where there is a small area of concrete in tension. The strain lines turn about point B.
• Range 5: Single or combined compression in which both materials are in compression. The strain lines turn about point C, as defined by the line corresponding to the ultimate compression strain of concrete, ε_c3, defined in paragraph 3.1.7.

The neutral axis "x" is an axis in the cross section which there are no longitudinal stresses or strains.

Deformation ranges correspond to all combinations of bending and axial force, from simple tensile to the simple compression, by varying the depth of the neutral axis "x" from - ∞ to + ∞ .

Checking rectangular sections

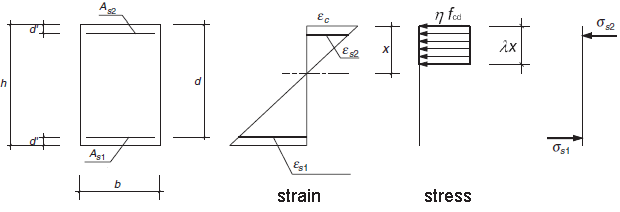
The equilibrium equations that determine the bending and axial force at failure (Mu and Nu) are the following
(Interaction diagram between axial load Ν and bending moment M)

Range 1:

- ∞ < x ≤ 0

• N_u(x) = - A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u (x)= - A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(d'-x)/(d-x)

Range 2:

0 < x ≤ d · ε_cu/(ε_cu+ε_ud)

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_ud]
• M_u(x)= η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_ud]·(h/2-d)
• ε_s2(x) = ε_ud·(x-d')/(d-x)

Range 3:

d · ε_cu/(ε_cu+ε_ud) < x ≤ x_lim

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Range 4:

x_lim< x ≤ d

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] - A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') - A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(d-x)/x

Range 4a:

d < x ≤ h

• N_u(x) = η·f_cd·λ·x·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u/x) = η·f_cd·λ·x·b·(h/2-λ·x/2) + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_cu·(x-d')/x
• ε_s1(x) = ε_cu·(x-d)/x

Range 5:

h < x < ∞

• N_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b + A_s2·σ_s2[ε_s2] + A_s1·σ_s1[ε_s1]
• M_u(x) = η·f_cd·[1- (1-λ)·h/x]·h·b·[h/2-[1- (1-λ)·h/x]·h/2] + A_s2·σ_s2[ε_s2]·(h/2-d') + A_s1·σ_s1[ε_s1]·(h/2-d)
• ε_s2(x) = ε_c3·(x-d')/(x-h/2)
• ε_s1(x) = ε_c3·(x-d)/(x-h/2)