Crack width and Stress limitation
RESULT
Maximum compressive stress in concrete
| Concrete compressive stress | Compression stress limit | Requirement |
| σc (MPa) | σc,max (MPa) | σc < σc,max |
| 10.88 | 18 | OK |
Maximum tensile stress in reinforcement
| Reinforcement tensile stress | Tensile stress limit | Requirement |
| σs1 (MPa) | σs1,max (MPa) | σs1 < σs1,max |
| 303.39 | 400 | OK |
Crack width
| Maximum crack spacing | Mean strain | Crack width |
| sr,max (cm) | εsm - εcm (‰) | Wk (mm) |
| 32.2 | 0.91 | 0.29 |
DETAILS OF CALCULATION
Notation and methodology according to clause 7 of EC2
Stress calculation assuming cracked section
- Stress in the tension reinforcement
σs1 = n·σc·(d-X)/X = 6.09·10.88·(25.9-4.64)/4.64 = 303.39 MPa - Maximun reinforcement tensile stress
σs1,max = k3 · fyk = 0.8 · 500 = 400 MPa - Compressive stress in the most compressed concrete fibre
σc = Mk · X / Icr = 10.88 MPa - Maximum compressive stress
σc,max = k1 · fck = 0.6 · 30 = 18 MPa
where
- n= Es / Ecm = 200 / 32.84 = 6.09
Ecm = 22·[fcm/10]0.3 = 22·[38/10]0.3 = 32.84 GPa
fcm = fck + 8 = 30 + 8 = 38 MPa - d (effective depth) = h – c - Φ/2 = 30 – 3.5 – 1.2/2 = 25.9 cm
- X (Depth of the neutral fibre) = 4.64 cm
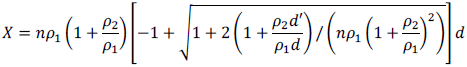
with:- d′ = h - d = 30 - 25.9 = 4.1 cm
- ρ1 = As1 / (b·d) = 3.39 / (40·25.9) = 0.0033
- ρ2 = As2 / (b·d) = 2.36 / (40·25.9) = 0.0023
- Icr (cracked inertia) = 10668.66 cm4
Icr = n·As1·(d-X)·(d-X/3) + n·As2·(X-d′)·(X/3-d′)
Icr = 6.09·3.39·(25.9-4.64)·(25.9-4.64/3) + 6.09·2.36·(4.64-4.1)·(4.64/3-4.1) = 10668.66 cm4
Calculation of crack width
wk = sr,msx·(εsm - εcm) = 322.5 · 0.00091 = 0.29 mm
where
εsm - εcm (difference between mean strains) = 0.00091
εsm - εcm = max(εm,1 ; εm,2) = max(0.0006 ; 0.00091)
with:
- εm,1 = [σs1 - kt·(fct,eff/ρp,eff)·(1+αe·ρp,eff)] / Es
εm,1 = [303.39 - 0.6·(2.9/0.01)·(1+6.09·0.01)] / 200000 = 0.0006
- kt = 0.6 (Long term loading)
- fct,eff = fctm = 2.9 MPa
fctm = 0,30 × fck(2/3) = 0,30 × 30(2/3) = 2.9 MPa - ρp,eff = As / Ac,eff = 3.39 / 338.1 = 0.01
Ac,eff = b · hc,ef = 40 · 8.45 = 338.1 cm2
hc,ef = min[2.5(h-d) ; (h-X)/3 ; h/2] = min[10.25 ; 8.45 ; 15] cm - αe = Es / Ecm = 6.09
- εm,2 = 0.6 · σs / Es = 0.6 · 303.39 / 200000 = 0.00091
sr,msx (Maximum crack spacing) = 32.25 cm
(case spacing = 170 mm ≤ 5(c+Φ/2) = 205 mm)
sr,msx = k3·c + k1·k2·k4·Φ/ρp,eff
sr,msx = 3.4·35 + 0.8·0.5·0.425·12/0.01 = 322.46 mm
with:
- k1 = 0.8 (high bond bars)
- k2 = 0.5 (bending)





