6.2 Shear

6.2.1 General verification procedure

(1)P For the verification of the shear resistance the following symbols are defined:

• V_Rd,c is the design shear resistance of the member without shear reinforcement.
• V_Rd,s is the design value of the shear force which can be sustained by the yielding shear reinforcement.
• V_Rd,max is the design value of the maximum shear force which can be sustained by the member, limited by crushing of the compression struts.

In members with inclined chords the following additional values are defined (see Figure 6.2):

• V_ccd is the design value of the shear component of the force in the compression area, in the case of an inclined compression chord.
• V_td is the design value of the shear component of the force in the tensile reinforcenlent, in the case of an inclined tensile chord.

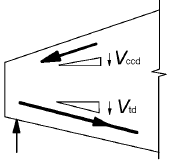
Figure 6.2: Shear component for members with inclined chords

(2) The shear resistance of a member with shear reinforcement is equal to:

(3) In regions of the member where V_Ed ≤ V_Rd,c no calculated shear reinforcement is necessary. V_Ed is the design shear force in the section considered resulting from external loading and prestressing (bonded or unbonded).

(4) When, on the basis of the design shear calculation, no shear reinforcement is required, minimum shear reinforcement should nevertheless be provided according to 9.2.2. The minimum shear reinforcement may be omitted in members such as slabs (solid, ribbed or hollow core slabs) where transverse redistribution of loads is possible. Minimum reinforcement may also be omitted in members of minor importance (e.g. lintels with span 2 m) which do not contribute significantly to the overall resistance and stability of the structure.

(5) In regions where V_Ed > V_Rd,c, according to Expression (6.2) sufficient shear reinforcement should be provided in order that V_Ed ≤ V_Rd (see Expression (6.1 )).

(6) The sum of the design shear force and the contributions of the flanges, V_Ed - V_ccd - V_td, should not exceed the permitted maximum value V_Rd,max (see 6.2.3), anywhere in the member.

(7) The longitudinal tension reinforcement should be able to resist the additional tensile force caused by shear (see 6.2.3 (7)).

(8) For members subject to predominantly uniformly distributed loading the design shear force need not to be checked at a distance less than d from the face of the support. Any shear reinforcement required should continue to the support. In addition it should be verified that the shear at the support does not exceed V_Rd,max (see also 6.2.2 (6) and 6.2.3 (8).

(9) Where a load is applied near the bottom of a section, sufficient vertical reinforcement to carry the load to the top of the section should be provided in addition to any reinforcement required to resist shear.

6.2.2 Members not requiring design shear reinforcement

(1) The design value for the shear resistance V_Rd,c is given by:

with a minimum of

where:

• f_ck is in MPa
• k = 1 + (200/d)^1/2 ≤ 2.0 with d in mm
• ρ₁ = A_s1/(b_w·d) ≤ 0.02
• A_s1 is the area of the tensile reinforcement, which extends ≥ (l_bd + d) beyond the section considered (see Figure 6.3).
• b_w is the smallest width of the cross-section in the tensile area (mm)
• σ_cp = N_Ed/A_c < 0,2 f_cd (MPa)
• N_Ed is the axial force in the cross-section due to loading or prestressing [in N] (N_Ed > 0 for compression). The influence of imposed deformations on N_Ed may be ignored.
• A_c is the area of concrete cross section [mm2]
• V_Rd,c is [N]

Note: The values of C_Rd,c, V_min and k₁ for use in a Country may be found in its National Annex. The recommended value for C_Rd,c is 0,18/γ_c, that for v_min is given by Expression (6.3N) and that for k₁ is 0,15.

Figure 6.3: Definition of A_sl in Expression (6.2)

(3) The calculation of the shear resistance according to Expression (6.4) is not required for cross-sections that are nearer to the support than the point which is the intersection of the elastic centroidal axis and a line inclined from the inner edge of the support at an angle of 45°.

(4) For the general case of members subjected to a bending moment and an axial force, which can be shown to be uncracked in flexure at the ULS, reference is made to 12.6.3.

(5) For the design of the longitudinal reinforcement, in the region cracked in flexure, the M_Ed - line should be shifted over a distance a₁ = d in the unfavourable direction (see 9.2.1.3 (2)).

6.2.3 Members requiring design shear reinforcement

(1) The design of members with shear reinforcement is based on a truss model (Figure 6.5). Limiting values for the angle θ of the inclined struts in the web are given in 6.2.3 (2).

In Figure 6.5 the following notations are shown:

• α is the angle between shear reinforcement and the beam axis perpendicular to the shear force (measured positive as shown in Figure 6.5)
• θ is the angle between the concrete compression strut and the beam axis perpendicular to the shear force
• F_td is the design value of the tensile force in the longitudinal reinforcement
• F_ed is the design value of the concrete compression force in the direction of the longitudinal member axis.
• b_w is the minimum width between tension and compression chords.
• z is the inner lever arm, for a member with constant depth, corresponding to the bending moment in the element under consideration. In the shear analysis of reinforced concrete without axial force, the approximate value z = 0,9d may normally be used.

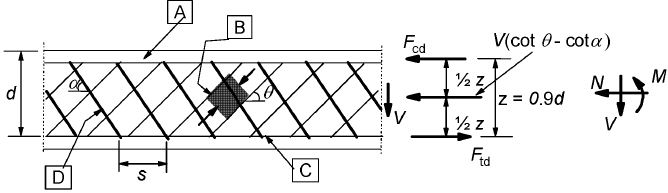
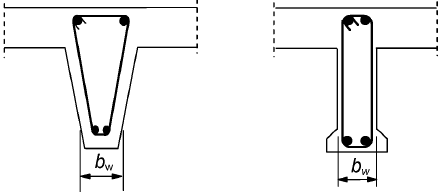
Figure 6.5: Truss model and notation for shear reinforced members

(2) The angle θ should be limited.

Note: The limiting values of cotθ for use in a Country may be found in its National Annex. The recommended limits are given in Expression (6.7N).

(3) For members with vertical shear reinforcement, the shear resistance, V_Rd is the smaller value of:

Note: If Expression (6.10) is used the value of f_ywd should be reduced to 0,8 f_ywk in Expression (6.8)

where:

• A_sw is the cross-sectional area of the shear reinforcement
• s is the spacing of the stirrups
• f_ywd is the design yield strength of the shear reinforcement
• v₁ is a strength reduction factor for concrete cracked in shear
• a_cw is a coefficient taking account of the state of the stress in the compression chord

Note 1: The value of v₁ and α_cw for use in a Country may be found in its National Annex. The recommended value of v₁ is v (see Expression (6.6N)).

, f_ck in MPa
(6.6N)

Note 2: If the design stress of the shear reinforcement is below 80% of the characteristic yield stress f_yk. v₁ may be taken as:

v₁ = 0.6 for f_ck ≤ 60 MPa
(6.10aN)
v₁ = 0.9 - f_ck/200 > 0.5 for f_ck > 60 MPa
(6.10bN)

Note 3: The recommended value of α_cw is as follows:

1 for non-prestressed structures


(1 + σ_cp/f_cd), for 0 < σ_cp ≤ 0.25 f_cd
(6.11aN)


1.25, for 0.25 f_cd < σ_cp ≤ 0.5 f_cd
(6.11bN)


2.5(1 - σ_cp/f_cd), for 0.5 f_cd < σ_cp ≤ 1.0 f_cd
(6.11cN)

where
σ_cp is the mean compressive stress, measured positive, in the concrete due to the design axial force. This should be obtained by averaging it over the concrete section taking account of the reinforcement. The value of σ_cp need not be calculated at a distance less than 0.5d cotθ from the edge of the support.

Note 4: The maximum effective cross-sectional area of the shear reinforcement, A_sw.max, for cotθ =1 is given by:

(6.12)

(4) For members with inclined shear reinforcement, the shear resistance is the smaller value of

Note: The maximum effective shear reinforcement, A_sw,max for cotθ =1 follows from:

(6.15)